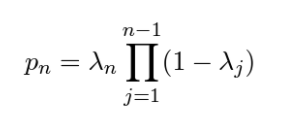PonderNet: Learning to Ponder (סקירה)

סקירה זו היא חלק מפינה קבועה בה אני סוקר מאמרים חשובים בתחום ה-ML/DL, וכותב גרסה פשוטה וברורה יותר שלהם בעברית. במידה ותרצו לקרוא את המאמרים הנוספים שסיכמתי, אתם מוזמנים לבדוק את העמוד שמרכז אותם תחת השם deepnightlearners.

לילה טוב חברים, היום אנחנו שוב בפינתנו deepnightlearners עם סקירה של מאמר בתחום הלמידה העמוקה. היום בחרתי לסקירה את המאמר שנקרא: 

PonderNet: Learning to Ponder

פינת הסוקר:  

        המלצת קריאה ממייק: מומלץ בעיקר להרחבת אופקים

        בהירות כתיבה:  גבוהה

        ידע מוקדם: הבנה בסיסית ברשתות ובחוקי הסתברות

        יישומים פרקטיים אפשריים: —

פרטי מאמר:

      לינק למאמר: זמין להורדה.

      לינק לקוד: לא רשמי 1, לא רשמי 2

      פורסם בתאריך: 02.09.2021, בארקיב (v2)

      הוצג בכנס: 8th ICML Workshop on Automated Machine Learning (AutoML 2021)

תחומי מאמר:

• מודלים (במקרה הזה רשתות נוירונים) בעלי זמן חישוב אדפטיבי (תלוי במורכבות משימה)

ידע מוקדם:

• מודלים (במקרה הזה רשתות נוירונים) בעלי זמן חישוב אדפטיבי (תלוי במורכבות משימה)
• מרחק KL בין התפלגויות
• התפלגות גיאומטרית 

תמצית מאמר:

המאמר הנסקר משתייך לתחום שלא הייתי מודע לקיומו עד שקראתי אותו. התחום דן ברשתות נוירונים שמסוגלות להתאים את כמות החישובים למשימה נתונה בהתאם לרמת המורכבות של המשימה. כלומר עבור המשימה "קלה" רשת כזו תבצע פחות חישובים מאשר למשימה "מורכבת יותר". 

המטרה העיקרית כאן היא להקנות למודל את היכולת להפסיק את תהליך האימון במצב בו נראה כי הוא ״הצליח ללמוד את מה הוא היה שצריך״, וממילא המשך האימון לא צפוי לשפר את ביצועי המודל באופן משמעותי. אם לעומת זאת המודל ״רואה״ כי איטרציות אימון נוספות עשויות להניב תוצאות טובות, הוא בוחר להמשיך את האימון. אציין כי רמת המורכבות של משימה אינה מועברת כקלט לרשת אלא הרשת צריכה "להחליט" on-the-fly עד כמה המשימה מסובכת ולהתאים את כמות החישובים הנדרשת. 

המאמר הנסקר מציע שיטה, הנקראת PonderNet, ההוכפת רשת נוירונים נתונה ל״אדפטיבית מבחינה חישובית״, כלומר כזו שיודעת להתאים את כמות החישובים לפי רמת המורכבות של בעיה. PonderNet דורשת שינויים קלים לארכיטקטורת הרשת, ו״מצליחה להשיג איזון בין ביצועי המודל על סט אימון, כמות החישובים הנדרשת ויכולת הכללה של הרשת" (לשון המאמר).

הסבר של רעיונות בסיסיים:

הרעיון של המאמר הוא די פשוט וטבעי. בהרצה הראשונה של הרשת מזינים לה את הקלט המקורי (נגיד, תמונה, טקסט או קטע אודיו) ומקבלים כפלט את הייצוג החבוי (ה"לטנטי") שלו. ייצוג לטנטי זה משמש כקלט להרצת רשת הבאה. לאחר מכן מריצים את הרשת פעם אחרי פעם כאשר הקלט hn(ייצוג חבוי – hidden state) לכל הרצה (איטרציה) הוא הפלט של האיטרציה הקודמת (n-1). בנוסף, לאחר כל איטרציה הרשת מספקת את החיזוי yn* עבור המשימה המקורית של הרשת ואת ההסתברות לעצירת הריצה n.  כלומר, פלט של רשת אחרי איטרציה n הוא השלישיה

 y*_n, λ_n, h_n = s(y*_n-1, λ_n-1, h_n-1),

כאשר s הוא מיפוי הממודל באמצעות רשת נוירונים כללית (LSTM, MLP, encoder-decoder). במאמר s נקראת פונקציית מדרגה (step function).

כעת נדון בדקות מעניינת לגבי ההסתברויות לעצירה …,λ_n, n=1, 2, כאמור λ_n מתארת הסתברות לעצירת ריצה של רשת באיטרציה n. באופן פורמלי λ_n היא הסתברות מותנית של עצירה בשלב n בהינתן אי עצירה (המשך) בשלב (n-1). זה, להבדיל מהסתברות לעצירה … ,p_n, n=1, 2  הבלתי מותנית לאחר איטרציה n שניתן לחשב אותה באופן הבא:

המאמר הנסקר מציין כי העבודות הקודמות ניסו לחזות דווקא את p_n ולא n.

נציין כי  …,p_n, n=1, 2 מגדירה התפלגות הסתברותית תקינה כאשר מספר האיטרציות המקסימלי אינו מוגבל. כמובן שזה עלול להיות בעייתי עבור שימושים פרקטיים של השיטה המוצעת. המאמר מציע שתי דרכים להתמודד עם סוגיה זו ונדון בהן בהמשך הסקירה. 

איך מתבצע חיזוי עם PonderNet: אחרי שהסברנו מה הרעיון שעומד מאחורי PonderNet נשאלת השאלה: איך בעצם מבצעים חיזוי עם הרשת הזו? כאמור, בכל איטרציה הפלט של הרשת מורכב מהחיזוי עבור המשימה המקורית, יחד עם האומדן של ההסתברות לעצירה לאחר האיטרציה הנוכחית n. אז איך אנו יודעים מתי לעצור את הריצה? פשוט מאוד – מבצעים דגימה אחת של משתנה בינארי עם הסתברות הצלחה n ומחליטים על סמך התוצאה האם לעצור או להמשיך. במילים אחרות אחרי כל איטרציה ״זורקים״ מטבע (לרוב לא הוגן) כאשר על צדדים של כתוב ״המשך״ ו״עצור״ כאשר הסתברות של ״עצור״ הוא n. במקרה של עצירה החיזוי האחרון yn*משמש כחיזוי סופי של PonderNet עבור המשימה שבנידון.

איך מאמנים PonderNet: פונקציית לוס של PonderNet בכל איטרציה …,n=1, 2 מורכבת משני איברים:

1. הלוס המקורי של משימת הרשת: לוס על ״איכות״ החיזוי y*_n, כמו למשל L(y*_n, y), כאשר y הוא הלייבל האמיתי (ground-truth). במאמר השתמשו בלוס הריבועי או בקרוס אנטרופי.
   
2. לוס נוסף עבור הסתברות עצירת האימון: איבר רגולריזציה בצורה של מרחק KL בין ההתפלגות pn לבין התפלגות פריור P_g. התפלגות P_g נבחרה ע״י המחברים בתור התפלגות גיאומטרית עם פרמטר מקונפג (היפרפרמטר). כמובן בשביל לחשב את מרחק KL בין pn לבין P_g צריך להריץ את PonderNet מספר מקסימלי של הרצות בלי לעצור אותו. למעשה לאיבר רגולריזציה זה יש שתי מטרות עיקריות: הראשונה ״לכפות״ על הרשת להיעצר לאחר 1/ הרצות (בממוצע) והשניה היא למנוע מרשת להוציא כפלט הסתברויות אפסיות לעצירה כל הזמן (סוג של עידוד exploration). 

נרמול של התפלגות  …,p_n, n=1, 2: כעת אספק הבהרה לגבי הסוגיה של נרמול ההתפלגות  …,p_n, n=1, 2 שהעלינו באחד הפרקים הקודמים. כאמור אנו לא יכולים להריץ את PonderNet לאורך מספר בלתי מוגבל של איטרציות ביישומים פרקטים. המאמר קובע את המספר המקסימלי של הרצות N, וקל לראות שהסדרה

p_n, n=1, 2, …,N כבר לא מהווה פונקציה התפלגות תקינה כי סכום של הסדרה אינו שווה ל- 1. המאמר מציע שתי דרכים לנרמול של p_n, n=1, 2, …,N:

1. לנרמל באופן סטנדרטי באמצעות חלוקה של כל pn בסכום של הסדרה.
2. ״להעביר״ את כל המסה ההסתברותית הנותרת לפני האיטרציה האחרונה להסתברות עצירה של האיטרציה האחרונה pN.

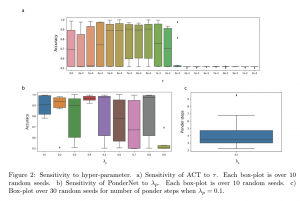
איך קובעים את מספר האיטרציות המקסימלי N: הנקודה המעניינת האחרונה שאני רוצה להתייחס אליה היא בחירה של מספר האיטרציות המקסימלי N. כמובן ניתן לאפטם אותו כמו כל היפרפרמטר אחר, אבל המחברים מציעים להגדיר אותו דרך "שארית של המסה הסתברותית לעצירה של הריצה". כלומר בוחרים מספר חיובי קטן c (במאמר בחרו ב- 0.05) ומגדירים את N כמספר המינימלי של איטרציות הנדרשות כדי שהסכום של …,p_n, n=1, 2 יהיה גדול יותר מ- 1- c). זה כמובן נעשה במהלך אימון של PonderNet.

הישגי מאמר: 

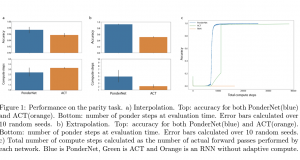
המחברים בחרו כמה משימות (שרובן "אינן מככבות" במאמרים בנושא הרשתות) והראו כי הביצועים של השיטה המוצעת עדיפה על גישות "אדפטיביות" האחרות עבור כמה ארכיטקטורות של פונקציית המדרגה s. למשל אחת המשימות היא חישוב של parity עבור סדרה בינארית ארוכה. ההשוואה התמקדה בעיקר בשיטה, הנקראת ACT, שכנראה נחשבה ל SOTA לפני כן.  המחברים הראו ש- PonderNet מצליח גם במשימות של question answering, הנקרא bAbI (המורכב מ- 20 תת-משימות שונות). השיפור בביצועים התבטא בדרך כלל ביכולת להגיע לאותן ביצועים בפחות זמן מאשר הגישות המתחרות. 

נ.ב.

לא הכרתי בעבר מאמרים הדנים במודלים בעלי זמן ריצה אדפטיבי והיה מגניב לצלול לנושא החשוב הזה. המאמר קל לקריאה, הרעיון העיקרי שלו אינטואיטיבי ומובן להפליא אולם נראה כי כרגע אין הרבה משימות ודומיינים שניתן ליישם אותו בהם. 

#deepnightlearners

הפוסט נכתב על ידי מיכאל (מייק) ארליכסון, PhD, Michael Erlihson.

מיכאל עובד בחברת הסייבר Salt Security בתור Principal Data Scientist. מיכאל חוקר ופועל בתחום הלמידה העמוקה, ולצד זאת מרצה ומנגיש את החומרים המדעיים לקהל הרחב.