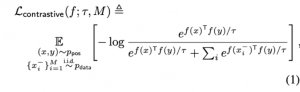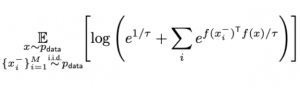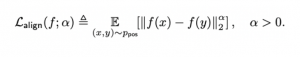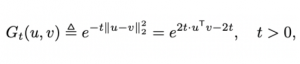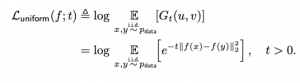Understanding Contrastive Representation Learning through Alignment and Uniformity on the Hypersphere: סקירה

סקירה זו נכתבה בשיתוף עם אלכסנדר מולק, Aleksander Molak.

סקירה זו היא חלק מפינה קבועה בה שותפיי ואנוכי סוקר מאמרים חשובים בתחום ה-ML/DL, וכותב גרסה פשוטה וברורה יותר שלהם בעברית. במידה ותרצו לקרוא את המאמרים הנוספים שסיכמנו שותפיי ואנוכי, אתם מוזמנים לבדוק את העמוד שמרכז אותם תחת השם deepnightlearners.

לילה טוב חברים, היום אנחנו שוב בפינתנו deepnightlearners עם סקירה של מאמר בתחום הלמידה העמוקה. היום בחרנו לסקירה את המאמר שנקרא: 

Understanding Contrastive Representation Learning through Alignment and Uniformity on the Hypersphere

פינת הסוקרים:

    המלצת קריאה מאלכסנדר וממייק: מומלץ מאוד לחובבי למידה self-supervised ולכל מי שמתעניין בלמידת ייצוג

    בהירות כתיבה: בינונית פלוס

    ידע מוקדם: 

• יסודות תורת ההסתברות ותורת המידה
• יסודות של למידה self-supervised ולמידה ניגודות 

    יישומים פרקטיים:

• ניתן להשתמש בגישה המוצעת להפקה של ייצוג דאטה טוב יותר מאשר בגישות הקודמות של למידה ניגודית.
  

  ---

פרטי מאמר:

    מאמר: כאן

    קוד: כאן

    פורסם בתאריך: ארקיב, 07.11.2020

    הוצג בכנס: ICML, 2020

תחומי מאמר:

• למידה ייצוגית (representation learning)
• למידה ניגודית (contrastive learning)

כלים מתמטיים, מושגים וסימונים:

• לוס ניגודי (Contrastive Loss)
• Radial Basic Function Kernel
• עקרון InfoMax 
• התכנסות חלשה (weak convergence) של מידות הסתברות.
  

  ---

   

מבוא:  

למידת ייצוג היא מונח גג למגוון שיטות המאפשרות לנו לבנות ייצוגי נתונים עוצמתיים שניתן לנצלם למשימות downstream מגוונות. דוגמה מצוינת ללמידת ייצוג היא word2vec – אלגוריתם self-supervised שהוצג ב-2013 על ידי Tomáš Mikolov ועמיתיו המשתמש בגישת הלמידה הניגודית. האלגוריתם בונה וקטורים של ייצוגי מילים (אמבדינגס) בעלי מאפיינים רצויים מסוימים, למשל מילים בעלות משמעות דומה ממופות לנקודות (וקטורים) קרובות במרחב הייצוג (embedding space). תכונה זו של ייצוג דאטה נקרא יישור (alignment). מודלי טרנספורמרים מרחיבים את היכולות של ייצוגי word2vec והופכים אותם לתלוים בהקשר. כלומר ייצוג של מילה נתונה תלוי במילים הקרובים אליה בטקסט. תכונה זו שדרגה את היכולות של מודלי שפה המבוססות על הטרנספורמרים אולם באותו הזמן וקטורי הייצוג שנוצרו באמצעות הטרנספורמרים סובלות צפיפות מאוד לא אחידה במרחב הייצוג. כלומר וקטורי הייצוג נוטים להתרכז באזור צר של מרחב הייצוג. תכונה זו עלולה לגרום למשל למה דנקרא ״קורלציות בדויות״ (Mimno & Thompson, 2017; Ethayarajh, 2019) כלומר קרבה בלתי רצויה בין ייצוגים של מילים לא קשורות הפוגע בביצועים של המודל. צפיפות ייצוגים לא אחידה מהווה בעיה גם בדומיינים אחרים כמו למשל הדומיין הויזואלי. המאמר הנסקר מנסה לתת מענה לסוגיה הזו.

תמצית מאמר:

המאמר הנסקר מראה כי ייצוגי דאטה, המופקים באמצעות מודלים שאומנו עם הלוס הניגודי (contrastive loss), עשויים להיות מאופיינים בשתי התכונות הטובות שהזכרנו קודם: אחידות ויישור (uniformity). לאחר מכן, הם מציעים פונקציית לוס המשפרת את המאפיינים הללו ולבסוף הם מראים שפונקציית לוס זו עתידה להוביל לייצוגים טובים יותר מאלה שהושגו באמצעות פונקציות לוס ניגודיות מסורתיות.

הסבר על הרעיון העיקרי:

למידה ניגודית היא אחת השיטות הנפוצות ביותר לבניית ייצוגי דאטה (בדרך כלל במרחב בעל ממד נמוך הנקרא לפעמים מרחב הלטנטי) עבור דאטהסטים לא מתויגים. הנחת היסוד מאחורי טכניקה זו היא שלדוגמאות דומות יש וקטורי ייצוגים קרובים, בעוד שלדוגמאות לא דומות יש וקטורי ייצוג מרוחקים. בפרט, ברוב שיטות הלמידה הניגודיות נבנים זוגות של דוגמאות דומות (חיוביות) וזוגות של דוגמאות לא דומות (שליליות) במהלך האימון. ביישומי ראייה ממוחשבת למשל, שני קרופים/סיבובים שונים של אותה תמונה יוצרים זוג חיובי בעוד שקרופים מתמונות שנבחרו באקראי יוצרים זוג שלילי. חלק משיטות הלמידה הניגודית לומדות את ייצוג הדאטה באמצעות מזעור היחס בין המרחקים בין ייצוגי זוגות חיוביים ושליליים. 

כאמור במאמר זה, המחברים בוחנים את המאפיינים של ייצוגי דאטה שאומנו באמצעות שיטות למידה המשתמשים בלוס הניגודי. המאמר מראה כי ייצוג דאטה המופקים במהלך הלמידה הניגודית יש שתי תכונות הבאות:

• יישור (alignment): קרבה בין ייצוגים של של פיסות דאטה קרובות.
• אחידות (uniformity): ייצוגי דאטה מפולגים באופן אחיד בהיפר-ספרה ברדיוס 1 (ראה הערה למטה). באופן אינטואיטיבי, אחידות של התפלגות הייצוגים במרחב הלטנטי מצביעה על כך שהייצוגים ״שומרים כמות מקסימלית של מידע״ של הדאטה המקורי.

הערה: המאמר מוסיף אילוץ של נורמה יחידה על ייצוגי דאטה. מספר עבודות קודמות מצאו כי אילוץ זה תורם לשיפור יציבות של תהליך האימון של שיטות למידה ניגודיות. כנראה שהסיבה לכך טמונה בשימוש ״כבד״ במכפלות פנימיות בפונקציות לוס של שיטות אלו. נציין כי למיטב ידיעתנו לא קיימת הוכחה ריגורוזית לכך שנורמה יחידה מהווה תכונה ״מועילה״ עבור ייצוגי דאטה.

התוצאה העיקרית של המאמר קובעת כי הלמידה הניגודית ממקסמת את שני המאפיינים שהוזכרו לעיל כאשר מספר הדגימות השליליות שואף לאינסוף. במילים פשוטות, כאשר מספר הדוגמאות השליליות במיני-באטץ' גבוה, אופטימיזציה של פונקציית הלוס הניגודית מובילה לייצוגי דאטה מיושרים ומפולגים באופן אחיד.

כמה עבודות ציינו כי הגדלת מספר הדוגמאות השליליות בשיטות למידה ניגודיות תורמת לשיפור של ייצוגי דאטה. מנקודת מבט זו, החלפת פונקציית מטרה של למידה ניגודית בכזו שמאפטמת אחידות ויישור הייצוגים באופן ישיר עשויה להוביל לייצוגי דאטה חזקים יותר. על מנת להטיל את אילוצי האחידות ויישור על וקטורי ייצוג דאטה, המחברים הציגו מדדים, מעוגנים תיאורטית, למדידת היישור והאחידות של הייצוגים. לבסוף המאמר הראה כי שילוב של הלוס המוצע (יישור ואחידות) יחד עם הלוס הניגודי, הצליח לייצר ייצוגי דאטה טובים יותר. 

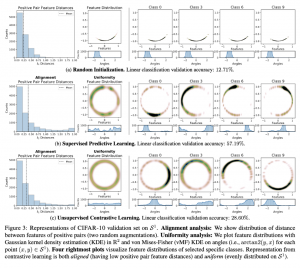
התמונה למטה ממחישה את תכונות היישור והאחידות החזקות של ייצוגי דאטה שנלמדו באמצעות למידה ניגודית  (2 תמונות משמאל בתחתית) על דאטהסט ללא תיוגים. מעניין לציין כי ייצוגי דאטה שנלמדו באמצעות למידה supervised (דאטה מתויג) מפגינות גם כן רמה גבוהה של אחידות ויישור (2 תמונות משמאל ביותר בשורה האמצעית).

פינת האינטואיציה:

בואו ננסה לספק קצת תובנות לגבי מדוע יישור ואחידות יכולים להיות מאפיינים טבעיים של ייצוג דאטה, שהופקו באמצעות למידה עם פונקציית הלוס הניגודית. קודם כל נתחיל מלרענן מהי פונקציית הלוס הניגודית (הצורה הנפוצה ביותר):

נניח שלדוגמאות חיוביות יש את אותו ייצוג / מיושרות בצורה מושלמת. נציין כי במקרה זה המכפלה הפנימית שלהם תהיה שווה ל-1, מכיוון נורמה של כל ייצוג שווה ל- 1. לכן הביטוי קודם מקבל את הצורה הבאה:

כאשר מספר הדוגמאות השליליות M גדול מאוד, המינימום של הביטוי האחרון מושג כאשר המרחקים בין זוגות של ייצוגים הוא מקסימלי (המכפלה הפנימית באקספוננט קרובה לאפס ככל האפשר). אז יישור ואחידות נראים כמאפיינים טבעיים של ייצוג דאטה המשיג ערך קטן של הלוס הניגודי.

המשפט העיקרי:

כעת נדון במשפט הראשי של המאמר:

המשפט קובע כי הלוס הניגודי שווה לסכום של 2 איברים הבאים כאשר מספר הדוגמאות השליליות M שואף לאינסוף (מעט מפושט לצורך הבהירות):

• איבר 1: ממוזער עבור ייצוג דאטה ״המיושרים״ בצורה מושלמת (הייצוגים של כל הזוגות החיוביים זהים).
• איבר 2: ממוזער כאשר הייצוגים מפולגים באופן אחיד.

איך לאמן ייצוגים מיושרים ומפולגים אחיד?

אז נראה שהחלפת לוס ניגודי בלוס המשלב אחידות עם יישור, מובילה לייצוגי דאטה חזקים יותר. שאלה היא כיצד אנו מאמנים מודל מסוגל להפיק ייצוגים עם תכונות אלו? המחברים מציעים לאכוף יישור ואחידות על הייצוגים באמצעות פונקציות לוס הבאות:

עבור יישור: לוס היישור מוגדר בתור מרחק ממוצע בין ייצוגים של זוגות חיוביים:

עבור אחידות: על מנת לאכוף אחידות על ייצוגי דאטה, המאמר משתמש במה שמכונה פונקציה רדיאלית גאוסית (הידועה גם כפונקציית בסיס רדיאלית או RBF). עם RBF, המרחק בין וקטורי ייצוג x ו-y מוגדר בצורה הבאה:

נציין כי השוויון השני נובע מהנורמה היחידה של וקטורי ייצוג x ו-y. עכשיו פונקציה לוס ״האוכפת״ אחידות מוגדרת בתור:

אבל למה שימוש בפונקצית לוס זו ״תפיק״ לנו ייצוגים מפולגים באופן יחיד? מסתבר (והמאמר מוכיח זאת) כי פונקציית הלוס מבוססת RBF ממוזערת כאשר וקטורי הייצוג המפולגים באופן אחד על היפר-ספרה בעלת רדיוס 1. בפשטות, עבור גודל מדגם (דאטהסט) גדול מאוד, וקטורי ייצוג הממזערים את פונקציית לוס זו "יכסו את פני השטח של היפר-ספרה היחידה באופן כמעט אחיד".

הערה: הן פונקציית לוס האוכפת אחידות והן זו האוכפת היישור של ייצוגים הינן פחות כבדות מבחינה חישובית מאשר הלוס הניגודי הסטנדרטי עקב היעדר פעולת softmax בו.

לכן אימון רשת נוירונים עם שילוב של פונקציות לוס הנ״ל נראה כדרך סבירה להשיג ייצוגי דאטה ומיושרים ומפולגים באופן אחיד.

הישגי מאמר: 

המחברים מצאו כי פונקציית לוס המצועת (אחידות + יישור) וגם שילובה ועם הלוס הניגודי הסטנדרטי הצליח להפיק ייצוגים חזקים יותר, וכתוצאה מכך השיג ביצועים טובים יותר במספר משימות downstream (סיווג ואומדני עומק) במספר דאטהסטים (כולל NYU Depth V2, ImageNet, ImageNet100, BookCorpus).

נ.ב.

במשך זמן רב, יישור ואחידות הוכרו כמאפיינים טובים של ייצוגי דאטה. המאמר הצליח להצביע על קשרים בין מאפיינים אלה לבין מספר שיטות אימון של למידה ניגודיות.

#deepnightlearners

הפוסט נכתב על ידי מיכאל (מייק) ארליכסון, PhD, Michael Erlihson ואלכסנדר מולק, Aleksander Molak.

מיכאל עובד בחברת הסייבר Salt Security בתור Principal Data Scientist. מיכאל חוקר ופועל בתחום הלמידה העמוקה, ולצד זאת מרצה ומנגיש את החומרים המדעיים לקהל הרחב.