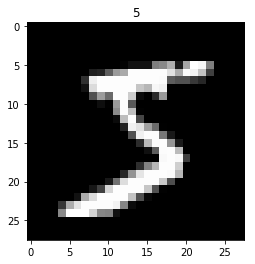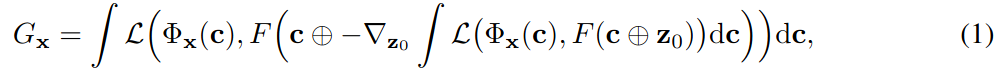Gradient Origin Networks – דרך חדשה ופשוטה למפות את המרחב הלטנטי

Gradient Origin Networks
Sam Bond-Taylor, Chris G. Willcocks
אמלק:
Gradient Origin Networks הן סוג חדש של רשתות שעוזרות לנו למפות את המרחב הלטנטי של דטה-סט מסויים, עם רשתות קטנות ופשוטות יותר לאימון מ-GANs ו-VAE. המאמר עושה זאת תוך כדי ניצול של התחום המגניב החדש שנקרא Implicit Representation Learning .
הקדמה:
אז כדי להבין את המשמעות של הרשתות האלה אנחנו דבר ראשון צריכים ללמוד על תחום שלם שאני כמעט ולא הכרתי אותו לפני שקראתי את המאמר: Implicit Representation. המטרה של התחום באופן כללי היא לייצג סיגנלים, כמו תמונות, מודלים תלת-מימדיים או כל סוג אחר של אותות בתור רשת נוירונים שממפה קואורדינטה במרחב של הסיגנל לערך של הסיגנל בקואוקדינטה הזאת.
מה זה אומר? קל להסביר את זה בתמונה:
נניח תמונה שהיא 32 על 32 פיקסלים ויש בתוכה את הספרה "5". המטרה היא לייצר רשת שמקבלת כל מיקום של פיקסל בתמונה ובתורה מוציאה ערך בין 0-1 לפי הערך של הפיקסל בתמונה שאנו מנסים לייצג. באופן זה, אנחנו מאמנים את הרשת כבעיית ריגרסיה פשוטה שמטרתה היא לסווג את הפיקסלים. אם ניתן לרשת בתור Input את הערכים (0,0) היא תביא לנו את הערך 0, ואם נביא לה את הערכים (7, 10) היא תביא לנו את הערך 1.
דרך פעולה זו טובה משתי סיבות מרכזיות:
א. זאת דרך למפות מידע (כלשהו) בהסתמך על מורכבות, ולא בהסתמך על הרזולוציה שלו. אם נרצה לשמור בפורמט PNG את אותו מספר "5" ברזולוציה פי 2 יותר גבוהה נצטרך פי 4 יותר זכרון, פה הרשת לומדת את המהות של הסיגנל ולכן יכול להכיל מידע בכל רזולוציה שנבחר לייצא.
ב. אנחנו יודעים לעשות מלא דברים עם רשתות. אנחנו יודעים לצמצם, לחקור ולהריץ אותן ביעילות על כל מיני פלטפורמות. דמיינו שלא משנה אם תפתחו משחק מחשב תלת-מימדי, תרנדרו תמונה מהאינטרנט או תפתחו מסמך וורד, מה שבעצם תורידו זאת רשת נוירונים שיודעת למפות מיקום (נקודת X,Y,Z בעולם המשחק, נקודות X,Y בתמונה או מיקום מילה במסמך) למשמעות (הפוליגון שבמיקום הזה, ערך ה-RGB או המילה עצמה).
אני לא ארחיב פה לעומק על המשמעויות הנוספות של התחום הזה ועל למה לדעתי הוא מאוד מבטיח, אבל לכל מי שרוצה להרחיב אני ממליץ לקרוא על SIREN Networks. זה מאמר שלדעתי בעתיד יחשב ממש מכונן ויש לו כמה טריקים מגניבים שעוזרים למפות את הדוגמאות בצורה יותר טובה, לדוגמא סינוס בתור אקטיבציה.
אז איך זה מתקשר ל-Gradient Origin Networks?
עכשיו דמיינו שבמקום שתרצו למפות תמונה אחת בתוך הרשת הזאת, תרצו למפות Dataset שלם. שיטה נאיבית לעשות את זה תהייה פשוט להוסיף עוד מימד. כמו שיש לנו X לרוחב התמונה ו-Y לגובה התמונה, ככה נוסיף Z למספר התמונה ב-Dataset. באופן זה נלמד את הרשת לקבל קואורדינטה מסוימת מתוך הגריד המדובר ולהחזיר את הערך בה. ככה הרשת תדע לקודד כל תמונה ב-Dataset. הבעיה בשיטה הנ"ל היא שבעוד קרבה במימדים של ה-X,Y מעידה על קרבה במהות (הרי אלה פיקסלים קרובים בתמונה ולכן יש ביניהם קשר) קרבה במימד ה-Z היא שרירותית. לכן, היינו רוצים תיאורטית להוסיף לרשת בנוסף ל-X,Y גם וקטור נוסף שקרבה בין שני וקטורים כאלה תראה גם על קרבה מהותית (כלומר, קרבה במרחב הלטנטי) בין התמונות. דרך טריויאלית תהיה לאמן Auto-Encoder שילמד לייצג את הוקטור הזה.
המאמר הזה לא עושה זאת ובעצם מציג דרך אחרת, מגניבה במיוחד, לייצר את הוקטור הזה.
במאמרים ב-Deep Learning אנחנו רגילים לקבל ציורים סכמטיים מושקעים של שכבות ושל רשתות אבל כאן הכותבים בחרו במקום זה לשים הנוסחא הזוועתית הבאה בתור הלוס שמתאר את המטרה של הרשת:
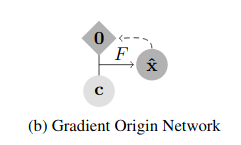
וכדי שנרגיש טיפה יותר טוב הם גם מוסיפים את האיור הסכמטי המאוד לא ברור הזה:
בתור בנאדם שהוא בבסיס איש של קוד, כשראיתי את זה ישר נכנסתי לגיטהאב של הפרויקט ודבר ראשון חקרתי אותו ואחר כך הרגשתי בנוח לחזור לנוסחא הזאת ולנסות להבין יותר לעומק מה היא אומרת.
נתחיל במה כל סימן אומר:
דבר ראשון F זאת הרשת שלנו, וסימו לב שאנחנו משתמשים בה פעמיים כשאנחנו מחשבים את ה-Loss
C – אלה הקורדינטות במרחב של הסיגנל, לדוגמא x,y בתמונה.
Φ – זה ה-Dataset כולו, מה שאומר שהסימון ϕx(c) אומר הערך של איבר מסויים ב-Dataset בקואורדינטה C. זה הערך שהרשת שלנו מנסה לחשב.
z0 – זה פשוט וקטור מלא אפסים
L – זה ה-Loss שלנו. במאמר הם משתמשים ב-L2, אבל זה יכול להיות תיאורטית כל פונקציית מרחק אחרת.
וכל השאר זה דברים שאנחנו מכירים מהעולם של רשתות ומתמטיקה באופן כללי, גרדיאנטים נגזרות ואינטגרלים.
נתחיל להבין את הנוסחא מבפנים החוצה:
F(c+z0) – אומר שניקח את הרשת שלנו ונכניס לה וקטור שמורכב מקונקטינציה של הקואורדינטות של הסיגנל במרחב, יחד עם וקטור אפסים. כעת, ניקח את התוצר, ונחשב את L2 בינו לבין הערך האמיתי של הנקודה הזאת באובייקט שאותו אנחנו מנסים למפות. מאחר ומדובר ברשת אנחנו יכולים לעשות טריק מאוד פשוט שהוא החידוש האמיתי במאמר:
נעשה Backword Pass על הרשת כולה עד שנגיע לגרדיאנטים שאמורים להשפיע על הוקטור Z0 שלנו. כעת ניקח את הערכים הנגדיים של הגרדיאנטים האלה (כמו שאנחנו עושים ב-Gradient descent) ונשתמש בהם בתור וקטור הייצוג שלנו. בשלב השני, נעשה להם שוב פעם קונקטינציה עם הקואורדינטות של הסיגנל שאנחנו מנסים לשחזר ונכניס עוד פעם לרשת שלנו, ואז מה שאנחנו מצפים זה באמת שיצא הערך של הדוגמא בקואורדינטה הזאת.
אוקיי, אני יודע שזה היה מסובך, אז מה עשינו פה בעצם? השתמשנו ברשת פעמיים: פעם אחת כדי להוציא ייצוג וקטורי ייחודי לתמונה, ופעם שנייה כדי להוציא את הערך של הפיקסל עצמו.
יש לזה שני יתרונות:
א. אנחנו משתמשים באותה רשת לשני שימושים שונים ובעצם חוסך בפרמטרים.
ב. אנחנו יכולים פשוט לאמן את הרשת מהתחלה ועד הסוף ב-Pass אחד, בלי להתחיל לאמן כמה רשתות שונות כמו ב-GANs.
אם נחזור לציור הסכמטי, אז עכשיו אפשר להבין אותו בפשטות: אנחנו לוקחים וקטור אפסים ומיקום קואורדינטות בתמונה ומוציאים את הערך בתמונה במיקום הזה וזאת על ידי הרצה כפולה של הרשת, פעם קדימה ופעם אחורה.
אז למה זה טוב?
א. אנחנו יכולים לאכסן עכשיו בצורה יעילה דאטא-סט שלם בתוך רשת, בדיוק כמו שקודם היינו מאחסנים סיגנל אחד. הוקטור הזה עוזר לנו לאחסן את המידע ככה שלקרבה יש משמעות וככה הרשת יכולה "לנצל" מבנים דומים בין סיגנלים דומים.
ב. (וזה החלק המגניב) אנחנו יכולים להתייחס לוקטור הזה בתור וקטור הייצוג במרחב הלטנטי, ואז אנחנו יכולים לעשות את כל השטויות שאנחנו עושים עם הוקטורים האלה ב-VAE או ב-GANS. לדוגמא, לקחת שתי דוגמאות ולעשות אינטרפולציה על הוקטורים שביניהם:
מה שמיוחד במאמר הזה זה שהוא ממש קצר (4 עמודים, מתוכם עמוד אחד הוא תמונות) ולא מובן כל כך. לדעתי חוסר הבהירות של המאמר נעשה בכוונה ואנחנו רואים פה ניסיון "לתקוע רגל בדלת" עם רעיון חדש ומקורי, שאין לי שום ספק שלקבוצה הזאת יש כבר לא מעט רעיונות לאיך לפתח אותו. זה נשמע לי כמו מאמר עם כמה רעיונות מאוד מקוריים שלדעתי ללא ספק עוד נראה איך משתמשים בהם בהמשך.
מאמר:
https://arxiv.org/pdf/2007.02798.pdf
קוד:
מחברת Colab להתנסות קלה:
https://colab.research.google.com/gist/cwkx/8c3a8b514f3bdfe123edc3bb0e6b7eca/gon.ipynb