A causal view of compositional zero-shot recognition (סקירה)

סקירה זו היא חלק מפינה קבועה בה אני סוקר מאמרים חשובים בתחום ה-ML/DL, וכותב גרסה פשוטה וברורה יותר שלהם בעברית. במידה ותרצו לקרוא את המאמרים הנוספים שסיכמתי, אתם מוזמנים לבדוק את העמוד שמרכז אותם תחת השם deepnightlearners.

לילה טוב חברים, היום אנחנו שוב בפינתנו deepnightlearners עם סקירה של מאמר בתחום הלמידה העמוקה. היום בחרתי לסקירה את המאמר שנקרא:

A causal view of compositional zero-shot recognition

פינת הסוקר:  

      המלצת קריאה ממייק: מומלץ בחום לבעלי ידע בתחומים רלוונטיים.

      בהירות כתיבה:  גבוהה.

      רמת היכרות עם כלים מתמטיים וטכניקות של ML/DL הנדרשים להבנת מאמר: נחוץ רקע טוב בהסתברות והבנה בסיסית של עקרונות הסיבתיות.

    יישומים פרקטיים אפשריים: אפשר להשתמש ברעיון זה בשביל לבנות מודל ליצירת דוגמאות (נגיד, תמונות) המכילות שילובים של אובייקטים שלא מופיעים בסט האימון.

פרטי מאמר:

      לינק למאמר: זמין להורדה.

      לינק לקוד: .זמין כאן

      פורסם בתאריך: 01.11.2020, בארקיב.

      הוצג בכנס: NeurIPSi 2020.

תחומי מאמר:

• למידת zero-shot ZS.
• הכללה הרכבתית (compositional generalization)- יכולת לזהות שילובים חדשים (שלא נראו ביחד קודם) של מרכיבים (פיצ'רים) ידועים.

כלים מתמטיים, מושגים וסימונים:

• הסקה סיבתית: גרף סיבתיות, פיצ'רים מערבבים (confounding), התערבות (intervention) לפיצ'רים.
• למידת ייצוגי דאטה מופרדים (disentangled representations).
• קריטריון מידע של הילברט-שמידט (HSIC): כלי שערוך של מידת אי תלות בין שני מדגמים של משתנים אקראיים.
• שערוך פריקות של ייצוגי דאטה לא מתויג (PIDA).

תמצית מאמר:

אחד האתגרים המשמעותיים בלמידת zero-shot זו הקניית יכולת הכללה הרכבתית למודל ZS. במילים אחרות אנו רוצים "ללמד" את המודל לזהות קומבינציות חדשות (!!) של מרכיבי דאטה בסיסיים שהוא הצליח לזהות בסט אימון (בעיקרון הכללה הרכבתית הינה מקרה פרטי של למידת ZS). בואו נתחיל מדוגמא של יכולת ההכללה ההרכבתית בדומיין הויזואלי. נניח שאתם מעולם לא ראיתם זאבים לבנים אך ברגע שתראו אחד, אתם בקלות תצליחו לזהות אותו כ "זאב לבן״ בגלל שאתם יודעים איך נראה זאב וגם אתם יודעים לזהות צבע לבן. זאת אומרת בזיכרון של בני אדם האובייקט ״זאב״ והתכונה (אטריביוט) ״לבן״ נשמרים בצורה נפרדת וקל לנו לשלב אותם גם אם הם מעולם לא ראו את השילוב שלהם(!!). לצערנו המודלים שמאומנים בצורה דיסקרימינטיבית מתקשים להפגין יכולת זו ויש שתי סיבות עיקריות לכך:

1. שינוי בהתפלגות בין סט אימון לטסט סט: המודל ״לא ראה״ את השילובים מהטסט סט במשך האימון. זה גרם לכך המודל למד קשרים בין פיצ'רים שמפריעים לו להרכיב אותם בצורה נכונה כאשר מריצים אותו על הטסט סט. למשל המודל שראה רק זאבים אפורים למד שיש קשר בין התכונה ״אפור״ לאובייקט ״זאב״ ועקב כך יתקשה לזהות זאבים בצבעים אחרים.
2.  ליבליים מעורבבים בסט אימון: המודל יתקשה "לפרק״ אותם למרכיבים הבסיסיים שלהם בהתבסס רק על הלייבלים. למשל אם הלייבל של תמונה הוא ״זאב אפור״, המודל המאומן בצורה דיסקרימינטיבית כנראה לא ״ישכיל להבין״ אילו פיצ'רים ויזואליים חשובים לזיהוי אובייקט ״זאב״ ואילו מגדירים את התכונה ״אפור״ 

המאמר מנסה להתגבר על קשיים אלו עי" הצעת מודל גנרטיבי M_g כאשר הקלט למודל הינו שילוב של אופייניים (לייבלים) של תמונה. למשל, כדי לגנרט תמונה של זאב לבן אנו נבחר את סוג האובייקט (זאב) ואת האטריבוט (לבן) ונייצר תמונה בהתבסס על אופייניים אלו. היתרון בגישה זו הוא שההתפלגות המותנית של תמונה, בשילובים של אופייניים אלו יהיה זהה בין סט האימון לטסט סט (!!). 

פינת האינטואיציה: שילוב של סוג אובייקט ואטריבוט של תמונה נוטה ליצור תמונות דומות גם בסט אימון וגם בטסט סט להבדיל מהתפלגות התמונות מותנות רק בסוג אובייקט או באטריבוט בנפרד. זה ההנחה המהותית שעליה מבוסס המאמר(!!).

אתם יכולים לשאול מה למודל הגנרטיבי הזה ולמשימות למידת ZS שהמאמר מנסה לפתור? התשובה הינה מאוד אינטואיטיבית –  "מאמנים" את המודל הגנרטיבי בתהליך הלמידה, כאשר בזמן ההסקה (אינפרנס) על תמונה x (המיוצגת עי" וקטור של פיצ'רים של x), אנו נבחר את שילוב האופייניים (a, o) הממקסם את ההסתברות המותנית של (P(x| a, o.  

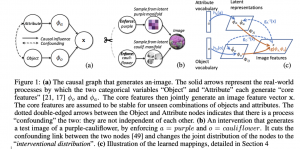
עד כאן הכל טוב ויפה אבל איך מתבצעות הלמידה וההסקה (בסגנון ZS) המתבססות על הנחות אלו בפועל? למטרה זו המאמר בונה גרף סיבתיות G המתאר את תהליך יצירת תמונות "אמיתיות". G ניתן לתיאור באופן הבא:

1.  בוחרים זוג של סוג אובייקט o ואטריבוט a ממרחב האובייקטים S_o ובמרחב האטריבוטים S_a בהתאמה. שימו לב ש- o ו- a הינם תלויים(!!) זה בזה (confounding). תלות זו הינה המכשול המרכזי בהקניית יכולת של ההכללה ההרכבתית למודלים דיסקרימינטיביים במשימות למידה ZS. האובייקטים והאטריבוטים ממודלים עי״ משתנים קטגוריאליים (ניתן לחשוב על S_o ועל S_a בתור מילונים של סוגי אובייקטים ושל אטריבוטים בהתאמה).
2.  אובייקט o ואטריבוט  a יוצרים פיצ'רי הליבה f_o ו- f_a. כמו שכבר אמרנו הנחת היסוד של המאמר אומרת שהתפלגויות של f_o ו- f_a אינן משתנות בין סט האימון לטסט סט.
3. פיצ'רי ליבה f_o ו- f_a יוצרים וקטור פיצ'רים g של תמונה (כלומר תמונה עצמה).

אבל איך גרף הסביבתיות המתואר קשור לבעיית למידה ZS , אתם שואלים? למעשה אנו צריכים למצוא דרך למדל שילובים בטסט סט שלא ראינו בסט האימון עי" שינוי של G. המאמר מציע לבצע את מה שנקרא בתורת ה "התערבות" (intervention) ל- G. אנו נאלץ את a ואת o לקבל ערכים ספציפיים ובכך "נקרע את התלות ביניהם". לאור זה הבעיה של ZS שהמאמר פותר ניתנת לניסוח הבא: מציאת התערבות לסוג אובייקט ואטריבוט שיצרה תמונה נתונה בסבירות הגבוהה ביותר.

הסבר של רעיונות בסיסיים:  אחרי שהבנו את העקרונות הבסיסיים של המאמר, הגיע הזמן לדבר על דרך מימוש של הגישה הזו. המטרה שלנו עבור תמונה נתונה מטסט סט הינה למצוא את הזוג של אובייקט o ושל אטריבוט a, הממקסם את ההסתברות המותנית של תמונה זו (P(x|o,a. 

הגדרות: כדי לפתור בעיה זו המאמר מגדיר שני מרחבים לטנטיים F_o ו- F_a המכילים ייצוגים לטנטיים של אובייקטים ואטריבוטים בהתאמה. אובייקט o יוצר התפלגות מותנית (P(f_o|o הממודל עי״ גאוסיאן עם המרכז (וקטור התוחלת) (h_o(o ומטריצת קווריאנס אלכסונית. ניתן לפרש את h_o בתור ייצוג אב טיפוס (פרוטוטייפ) של אובייקט o. ייצוג לטנטי של אטריבוטים a , המסומן f_a, מוגדרים באופן דומה. נציין שהמאמר מניח שההתפלגות (p(f_a|a ו- (p(f_o|o הינן זהות בין סט האימון לטסט סט. 

וקטור פיצ'רים של תמונה x מוגדר כגאוסי עם וקטור תוחלת (g(f_a, f_o  ומטריצת קווריאנס אלכסונית קבועה גם כן. כרגיל בתהליך האימון של מודלים גנרטיביים אנו צריכים גם למדל את ההתפלגות האפוסטריורית של וקטורי ייצוג לטנטיים של f_o ו- f_a (בהינתן וקטור פיצ'רים של תמונה x). מודלים אלו יסומנו עי״ g_io ו- g_ia בהתאמה. 

לאחר שסיימנו עם ההגדרות, נוכל לעבור לתיאור של תהליך הלמידה. המטרה של תהליך הלמידה הינה לאמן 5 רשתות (כולן מסוג MLP) שהן h_a, h_o, g, g_ia, g_io. פונקציה הלוס L מורכבת מ- 3 חלקים:

1. לוס על נראית הדאטה L_like: עבור תמונה בסט אימון מתויגת עם סוג אובייקט o ואטריבוט a בונים לוס המורכב מ 3 מחוברים:
   1. איבר שמוודא שהשערוך של הייצוג הלטנטי של סוג אובייקט o הניתן עי״ הרשת (g_io(x מקרב בצורה טובה את הייצוג פרוטוטייפ h_o של o. הקרבה נמדדת כאן כהפרש ריבועי בין h_o לבין (g_ia(x.
   2. איבר המשערך את המרחק הריבועי בין (g_ia(x לבין הפרוטוטייפ שלו h_a.
   3. טריפלט לוס כאשר העוגן (anchor) הינו וקטור פיצ'רים של התמונה x, הדוגמא החיוביות זה הזוג (a, o) האמיתי של התמונה (התיוג), והדוגמא השלילית זה זוג של אובייקט ואטריבוט אקראיים. פונקצית המרחק כאן הינה המרחק האוקלידי הריבועי בין x ל- (g(a, o.  נזכיר שהמטרה של טריפלט לוס הינה מינימיזציה של מרחק בין העוגן לדוגמא החיובית ומקסום המרחק בין העוגן לדוגמא השלילית. במקרה שלנו אנו רוצים ליצור תמונה בעלת פיצ'רים קרובים ל x בהינתן סוג האובייקט והאטריבוט שלה ולמקסם מרחק בין x לפיצ'רים של תמונה הנוצרת עי" זוג של אובייקט/אטריבוט אקראי.
2. חלק 2 של הלוס L_indep:  מנסה למעזר את התלות המותנית בין פיצ'רי ליבה f_a ו- f_o בהינתן סוג האובייקט/אטריבוט. למשל, הגרף הסיבתי בציור 1a מכתיב את אי התלות בין פיצ'ר ליבה f_o לאטריבוט a בהינתן האובייקט הנבחר o. ד"א המאמר מציין שאי תלות זו קשורה למטריקה המודדת את מידת הפריקות (disentanglement) של ייצוגי דאטה לא מתויגת (PIDA). בנוסף f_a צריך להיות בלתי תלוי ב f_o גם בהינתן האובייקט הנבחר o, ובנוסף אותה אי תלות צריכה להתקיים בהינתן אטריבוט o. מכיוון שאנו לא יכולים לדגום המרחבים הלטנטיים F_o ו- F_a, אנו מנסים לכפות את האי תלויות המותנות אלו בין השערוכים אפוסטריוריים שלהם הניתנים עי" (g_ia(x ו- (g_io(x. אבל איך בונים לוס הממזער את תלות סטטיסטית בין מדגמים של וקטורים אקראיים? כמובן, קורלציה פשוטה בין הוקטורים אינה מספקת כאן כי היא מודדת רק את התלות הלינארית בין הווקטורים. קיימות שיטות פרמטריות המבוססות על המידע הדדי, יש שיטות המבוססות על אימון אדוורסרי, אבל המאמר בחר בשיטה לא פרמטרית הנקראת קריטריון המידע של הילברט-שמידט (HSIC). בלי להיכנס יותר מדי לפרטים המתמטיים (HSIC זה יצור די מורכב) ניתן לחשוב על קריטריון זה כהכללה מסוימת של קורלציה בין וקטורים כאשר הוקטורים עוברים איזושהי טרנספורמציה לא לינארית (קרנל). אציין ש- L_indep מורכב מ- 4 ביטויי HSIC (אנו רוצים לכפות אי תלות מותנית בין 4 זוגות של פיצ'רי ליבה, אובייקטים ואטריבוטים (חלק מהם פורטו בתחילת הסעיף).
    
3. חלק 3 של הלוס L_invert: מנסה לאלץ את אמבדינגס h_a, h_o והווקטור פיצ'רים של תמונה (g(h_a,h_o להכיל כמה שיותר אינפורמציה על הלייבלים האמיתי של תמונה, a ו- o. אם זה לא יעשה h_a ו- h_o עלולים להתכנס לפתרונות טריוויאליים כי אין לנו גישה לערכים אמיתיים של הפיצ'רים הלטנטיים  f_a ו- f_o (ראה את ההסבר על הלוס הראשון L_like). אז עושים את הדבר הבא:

• • מוסיפים שכבת לינארית h_a ו- h_o לסיווג של אטריבוט וסוג אובייקט בהתאמה (כל אחד מקבל שכבה לינארית משלה ומאומן בנפרד) ומאמנים כל אחד מהם עם קרוס-אנטרופי לוס (שני לוסים).
  • מוסיפים שכבה לינארית לרשת הייצוג g לסיווג של סוג אובייקט ושכבה לינארית לסיווג של אטריבוט ומאמנים אותם עם אותו קרוס אנטרופי לוס (שני לוסים).
  • הלוס L_invert מורכבת מסכום של 4 הלוסים המתוארים בסעיפים הקודמים.

הדבר האחרון שנותר לנו לדון כאן זה האופן שבו מתבצעת ההסקה (אינפרנס). 

איך עושים אינפרנס: כמו שכבר אמרנו אנו מנסים למצוא זוג של (a, o) הממקסם את את ההסתברות של תמונה נתונה x. המאמר מראה כי (log p(x|a, o – ניתן לקרב על סכום של 3 האיברים הבאים:

1. מרחק ריבוע בין (g_ia(x לפרוטוטייפ h_a של a (כל הרשתות כאן אומנו בשלב הלמידה). מרחק זה מבטא ״עד כמה התמונה מכילה אטריבוט a המשוערך עי״ קרבתו של שערוך פיצ'ר ליבה f_a של x המשוערך עי״  (g_ia(x.
2. מרחק ריבוע בין (g_io(x לפרוטוטייפ h_o של o. 
3. המרחק הריבועי בין (g(h_a, h_o לבין התמונה x המבטא עד כמה מדויק ניתן לשחזר תמונה x מהזוג של (a, o)

בסוף בוחרים זוג (a, o) הממקסם את  (log p(x|a, o.

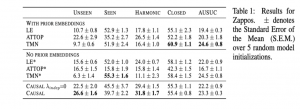
הישגי מאמר: המאמר מראה שיפור בביצועים על משימות ZS על דאטה סטים MIT states ו- UTZappos50K והדאטהסט הסינטטי AO-CLEVR מול כמה שיטות ZS כמו VisProd, ATTOP, TMN.

נ.ב. מאמר מאוד מעניין המציע שיטה של למידת ZS הנותנת מענה לקשיים שחווים מודלים דסקריפטיביים בזיהוי שילובים חדשים (לא מופיעים בסט אימון) של אופיינים בטסט סט. המאמר מציע מסגרת סיבתית בשביל להתגבר על הקושי הזה ומצליח להשיג שיפור ניכר בביצועים על משימות ZS על 3 דאטהסטים. המאמר משתמש בכלים מתמטיים די כבדים אך כתוב בצורה מאוד ברורה הנותנת לקורא להבין בקלות את הרעיון העיקרי. בקיצור המלצת קריאה ממני!

deepnightlearners#

הפוסט נכתב על ידי מיכאל (מייק) ארליכסון, PhD.

מיכאל עובד בחברת סייבר Salt Security בתור Principal Data Scientist. מיכאל חוקר ופועל בתחום הלמידה העמוקה, ולצד זאת מרצה ומנגיש את החומרים המדעיים לקהל הרחב.