Neuron Shapley: Discovering the Responsible Neurons (סקירה)

סקירה זו היא חלק מפינה קבועה בה אני סוקר מאמרים חשובים בתחום ה-ML/DL, וכותב גרסה פשוטה וברורה יותר שלהם בעברית. במידה ותרצו לקרוא את המאמרים הנוספים שסיכמתי, אתם מוזמנים לבדוק את העמוד שמרכז אותם תחת השם deepnightlearners.

לילה טוב חברים, היום אנחנו שוב בפינתנו deepnightlearners עם סקירה של מאמר בתחום הלמידה העמוקה. היום בחרתי לסקירה את המאמר שנקרא: 

Neuron Shapley: Discovering the Responsible Neurons

פינת הסוקר:  

           המלצת קריאה ממייק: כמעט חובה (לא חייבים אך ממש מומלץ).

          בהירות כתיבה:  בינונית פלוס.

          רמת היכרות עם כלים מתמטיים וטכניקות של ML/DL הנדרשים להבנת מאמר: היכרות בסיסית עם שיטות explainability כמו SHAP והבנה של מושגים סטטיסטיים בסיסיים כמו רווח סמך.

         יישומים פרקטיים אפשריים: זיהוי נוירונים המשפיעים ביותר על ביצועי רשת.

פרטי מאמר:

      לינק למאמר: זמין להורדה.

      לינק לקוד: זמין כאן

      פורסם בתאריך: 13.11.20, בארקיב.

      הוצג בכנס: NeurIPS 2020.

תחומי מאמר:

• חקר התנהגות של רשתות, נוירונים מאומנות, תורת המשחקים.

כלים מתמטיים, מושגים וסימונים: 

• ערכי SHAP.
• שיטת מונטה קרלו לדגימה.
•  בעיות שודדי מרובי ידיים.
• רווח סמך (confidence interval). 
• חשיבות של פיצ'רים (feature importance).
  

  ---

תמצית מאמר:  

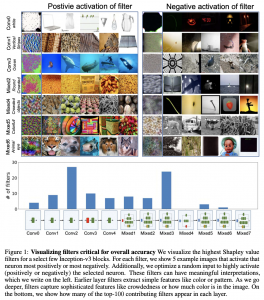
המאמר מציע שיטת למדידת תרומה של נוירון נתון על רשת נוירונים מאומנת על ביצועי הרשת. הרעיון בגדול הוא פשוט מאוד: אם איפוס של נוירון גורם לירידה משמעותית בביצועים של רשת הנוירונים, החשיבות (תרומה) של נוירון זה היא גבוהה, אחרת היא נמוכה. במידה מסוימת זה מזכיר "חשיבות של פיצ'ר" (feature importance) רק שכאן אנו בוחנים את הפיצ'רים של המודל עצמו ולא את התכונות של הקלט. המחברים בחרו בגישה דומה לערכי SHAP הקלאסיים, שהפכו לאחרונה לאחד הכלים הפופולריים בשערוך חשיבות הפיצירים, ככלי למדידת לחשיבות של נוירונים. באופן לא מפתיע "חשיבות של נוירון" נקראת במאמר ערך שאפלי של נוירון (Neuron Shapley – נקרא לזה N-Shap בהמשך).

אז מה זה בעצם N-Shap? למעשה ערך N-Shap של נוירון N_i מודד את התרומה הממוצעת לביצועי הרשת, מושגת עי״ הוספת נוירון N_i לכל תת-הרשתות של רשת N, שלא מכילות את N_i. כלומר לוקחים כל תתי-רשת של הרשת המאומנת N ,מודדים את הביצועים שלה ואז מוסיפים לכל אחת מהם את N_i, שוב מודדים את הביצועים ובסוף מחשבים את ההפרש בין הביצועים של רשתות אלו. נדגיש שאנו לא מאמנים את תת-הרשתות אלא רק מודדים את הביצועים שלהן על דאטהסט נתון. כלומר ערך N-Shap של נוירון N_i מוגדר כממוצע של הפרשי הביצועים עבור כל תתי-רשתות של N. שימו לב שבנוסחה (1) במאמר, המגדירה את N-Shap באופן פורמלי, מופיעות מקדמים בינומיים המשמשים לחישוב של מספר תת-רשתות בגודל S.

כידוע המספר הכולל של תת-רשתות של רשת נוירונים הינו אקספוננציאלי במונחי מספר הנוירונים ברשת. לכן גישה זו אינה ישימה אפילו עבור רשתות לא גדולות במיוחד (מאות אלפי נוירונים). כדי להתגבר על בעיה זו מחברי המאמר מציע שתי גישות: 

• גישת מונטה-קרלו: עבור כל נוירון N_i, דוגמים מספר תת-רשתות M (למעשה מגרילים את הנוירונים המרכיבים רשתות אלו) באופן רנדומלי, כלומר כל תת רשת מקבלת הסתברות שווה להיבחר. אז N-SHAP של כל נוירון זה בעצם ממוצע של כל התרומות של על כל תתי-הרשתות שנדגמו עבורו. מכיוון שמספר תתי רשתות הינו אקספוננציאלי במספר המשקלים ברשת הגישה הזו לא יעילה עקב השונות הגבוהה של האומדנים של N-Shap המחושבים באמצעותה (כאשר מספר הדגימות M הינו הרבה יותר קטן ממספר הנוירונים הכולל N_num).
• גישת דגימה אדפטיבית המבוססת על הכלים מעולם MAB: המאמר מציין כי למעשה אנו מעוניינים לאתר K נוירונים בעלי ערכי N-Shap הגבוהים ביותר. עם ניסוח כזה הבעייה הופכת דומה לבעיה הקלאסית בתחום של MAB קרי מציאת "מכונת הימורים בעלת הסתברות זכייה מקסימלית". ניתן לראות כי בעיה זו שקולה למציאה של K משתנים מקריים בעלי תוחלת הגבוהה ביותר מתוך סט גדול של משתנים אקראיים. בעיה זו נדונה באופן נרחב בספרות של MAB. 

בהתבסס על הבחנה זו המאמר מציע אלגוריתם הנקרא (truncated MAB ,Shapley T-MAB-S) שעבור K נתון מזהה K נוירונים עם התרומה הגבוהה ביותר. בגדול בכל איטרציה, עבור כל נוירון דוגמים תת-רשת אחת, מחשבים את תרומתו עבור תת-רשת זו ומעדכנים את הממוצע, השונות ורווח הסמך של נוירון זה. לאחר מכן מצמצמים את סט הנוירונים הנדגמים עי״ הוצאת נוירונים שרווח סמך שלהם של תרומתם לא מכיל את ערך התרומה ה-K המקסימלי (k-th largest) עבור אותה איטרציה. תרומת הנוירונים שהוצאו (התוחלת והשונות) נשארת קבוע לאורך כל האיטרציות הבאות. האלגוריתם עוצר כאשר לא נותרו נוירונים בסט הנדגם (התהליך והאינטואיציה יפורטו בפרק הבא).

הסבר של רעיונות בסיסיים:

פריטים ואינטואציה של האלגוריתם המוצע T-MAB-S: 

• מגדירים את סט הנוירונים הנדגמים U כסט המכיל את כל הנוירונים של רשת N.
• עבור כל נוירון N_i האלגוריתם דוגם תת-רשת אחת ומודדים את התרומה של N_i עבור תת רשת זו. נציין שאם הביצועים של לתת-הרשת שהוגרלה, הם מתחת לסף (הנקבע מראש), תרומתו באיטרציה זו נקבעת לאפס.
• אחרי כל איטרציה מחשבים את ממוצע, שונות ורווח-סמך של ערכי N-Shap עבור כל הנוירונים מ-U, בהסתמך על הערכים שהתקבלו באיטרציות הקודמות. נזכיר כי רווח סמך נבנה סביב הממוצע ורוחבו נמדד במספר שונויות סביב התוחלת (ראה הסבר על בניית רווח סמך ליותר פרטים).
• מחשבים את הערך K-th המקסימלי Max_K עבור ערכי N_Shap שהתקבלו באיטרציה זו.
• מוציאים מ-U את כל הנוירונים Max_K לא שייך לרווח סמך שלהם (עם איזשהו מרג'ין קטן משני הצדדים). ערכי N_Shap של נוירונים אלו נותרים ללא שינוי לאורך איטרציות הבאות.
• עוצרים כאשר סט הנוירונים הנדגמים נהיה ריק.
• בוחרים K הנוירונים עם ערכי N-Shap המקסימליים.

פינת האינטואיציה: למעשה Max_K הינו אומדן של מקסימום ה-K של כל ערכי N-Shap שנדגמו. כאשר אנו מוציאים את הנוירונים, שעבורם Max_K לא שייך לרווח סמך שלהם (האינטרוול שבו ערך N_Shap של נוירון טופ-K אמור להימצא בהסתברות גבוהה), אנו מוציאים את הנוירונים שהסבירות שערך N-Shap שלהם יהיה בין טופ-K הינה נמוכה. כך מצמצמים את מספר הנוירונים הנדגמים עי״ הוצאתם של ״מועמדים לא טובים להיות בין טופ-K״.

תכונות של N-Shap: כעת נדון בשלוש תכונות הבסיסיות של מטריקת N-Shap:

• ערך N-Shap אפס לנוירון N_i שקול לכך שהוספתו לכל תת-רשת לא משפיע בכלל על ביצועי הרשת.
• אם התרומות של שני נוירונים לכל תת-רשת אפשרית (שלא מכילה את שני נוירונים אלו) הינן שוות, אז ערכי N-Shap של נוירונים אלו שווים גם כן.
• אדיטיביות: נניח שיש לנו שני דאטהסטים שחישבנו עבורם ערכי N-Shap של נוירון כלשהו. ניתן לראות כי ערך N-Shap עבור נוירון זה המחושב על איחוד דאטהסטים אלו יהיה שווה לסכום של ערכי N-shap שלו.

בזכות תכונות אלו (שהמאמר הנסקר מוכיח בצורה ריגורוזית), נטען במאמר כי N-Shap מהווה מטריקה ״טובה והגיונית״ למדידה של תרומת נוירון לביצועי רשת (אני חושב ש-N-Shap הינה מטריקה טובה בהקשר המדובר כי היא מהווה הרחבה טבעית של ערכי שאפלי קלאסיים לרשתות נוירונים).

הסבר על מושגים חשובים במאמר:

ערכי שאפלי: ערכי שאפלי הינו כלי קלאסי לשערוך של חשיבות של פיצ'רים בהינתן מודל מאומן. למעשה עושים משהו מאוד דומה לנעשה במאמר הנסקר – מודדים את השינוי בביצועים המתקבל עי״ הוספת של פיצ'ר f לכל תת-קבוצה של פיצ'רים (כאשר יש מספר רב של פיצ'רים משתמשים בקירובים בצורה דומה למה שנעשה במאמר).

תיאור קצר של בעיית ״שודד מרובה ידיים״ (MAB): נניח שיש לנו N מכונות מזל שלכל אחת יש הסתברות שונה לזכייה והסתברויות אלו לא ידועה למהמר. המטרה העיקרית בבעיות MAB הינה (בגדול מאוד) למקסם את הרווח הממוצע של המהמר (הסבר מפורט על בעיות MAB).

הישגי מאמר:

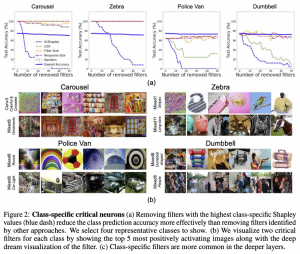
המאמר מראה כמה תוצאות מעניינות ודי לא צפויות לגבי ההשפעה של נוירונים טופ-K על ביצועים המודל (עבור רשת InceptionV3 שאומנה על Imagenet). למשל המאמר מראה כי הוצאתם של 10 נוירונים בלבד (למעשה זה איפוס של 10 קרנלים שמחשבים אותם) גורמת לירידה של 50% (!!) בדיוק כאשר האיפוס של 20 נוירונים כאלו מרסק את הביצועים ל-8% (!!) דיוק. עוד דבר מעניין שהמחברים מצאו: אם מוציאים את הנוירונים החשובים לזיהוי של קטגוריה ספציפית, הדיוק של קטגוריה זו מתרסק ואילו הפגיעה בדיוק בקטגוריות האחרות היא די קטנה. צריך לציין שהמסקנות האלו הן לא אינטואיטיביות כלל (לפחות מבחינתי)- הרי כאשר מאמנים רשת עם דרופאאוט חשיבות של כל נוירון בודד נוטה להיות לא גבוהה במיוחד. לא הייתי משער שההורדה של 20 נוירונים בלבד תוביל לקריסה מוחלטת של ביצועים.

בנוסף המאמר בדק מיהם הנוירונים ״הכי רגישים להתקפות אדוורסריות״, כלומר האם ניתן להתגונן נגד התקפה נתונה באמצעות ״איפוס״ של נוירונים מסוימים. נזכיר כי התקפה אדוורסרית מנסה להנדס שינוים קלים ולא נראים לעין לתמונה במטרה לגרום לרשת לשנות את החיזוי של התמונה באופן משמעותי. המחברים מצאו כי איפוס של נוירונים עם התרומה הכי גבוהה בהקשר הזה מצליח לנטרל את ההתקפה כמעט לגמרי ואילו הביצועים של הרשת על הדוגמאות הרגילות סופגות ירידה קלה בלבד. שימו לב שגישה זו אינה מהווה דרך טובה להתגונן נגד התקפות אדוורסריות. איפוס נוירונים הכי חשובים (בהקשר זה) מעניק הגנה נגד ההתקפה הספציפית בלבד(!!) וניתן די בקלות לבנות התקפות דומות אחרות כנגד רשת עם ״הנוירונים המאופסים״. כנראה שההתקפה החדשה תבחר נוירונים אחרים בשביל ״להתמקד עליהם״. מעניין שהנוירונים בעלי התרומה הכי גבוהה בהקשר האדוורסרי והנוירונים בעלי ערכי N-Shap הגבוהים ביותר עבור משימת הסיווג המקורית, יצאו די שונים.

נ.ב. 

מאמר מעניין המשלב שיטות מתחום MAB וערכי שאפלי לאנליזה של ״מה שקורה בתוך רשתות נוירונים מאומנות״. התוצאות של המאמר לא כל כך אינטואיטיביות והייתי שמח לראות עוד מאמרים בודקים את הסוגייה הזו על יותר משימות וארכיטקטורות רשת אחרות.

#deepnightlearners

הפוסט נכתב על ידי מיכאל (מייק) ארליכסון, PhD, Michael Erlihson.

מיכאל עובד בחברת הסייבר Salt Security בתור Principal Data Scientist. מיכאל חוקר ופועל בתחום הלמידה העמוקה, ולצד זאת מרצה ומנגיש את החומרים המדעיים לקהל הרחב.