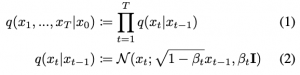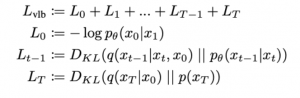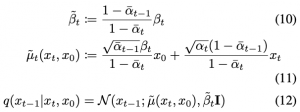Diffusion Models Beat GANs on Image Synthesis (סקירה)

סקירה זו היא חלק מפינה קבועה בה אני סוקר מאמרים חשובים בתחום ה-ML/DL, וכותב גרסה פשוטה וברורה יותר שלהם בעברית. במידה ותרצו לקרוא את המאמרים הנוספים שסיכמתי, אתם מוזמנים לבדוק את העמוד שמרכז אותם תחת השם deepnightlearners.
לילה טוב חברים, היום אנחנו שוב בפינתנו deepnightlearners עם סקירה של מאמר בתחום הלמידה העמוקה. היום בחרתי לסקירה את המאמר שנקרא:
Diffusion Models Beat GANs on Image Synthesis
פינת הסוקר:
המלצת קריאה ממייק: חובה למי שרוצה ללמוד מודלים גנרטיביים פרט לגאנים ול-VAE.
בהירות כתיבה: בינונית.
רמת היכרות עם כלים מתמטיים וטכניקות של ML/DL הנדרשים להבנת מאמר: הבנה טובה של עקרונות VAE, הבנה של שיטות דגימה מתקדמות כמו דינמיקה של לנגבין.
יישומים פרקטיים אפשריים: יצירת תמונות יותר "איכותיות" מהגישות המתחרות, קרי גאנים ו-VAE.
פרטי מאמר:
לינק למאמר: זמין להורדה.
לינק לקוד: זמין כאן
פורסם בתאריך: 01.06.21, בארקיב.
הוצג בכנס: טרם ידוע.
תחומי מאמר:
- מודלים דיפוזיוניים כלומר Diffusion Denoising Probabilistic Models – DDPM לגנרוט של דאטה ויזואלי.
ידע מוקדם:
- הבנה טובה בטכניקות מבוססות -variational inference לניתוח פונקציות נראות מירבית (כמו ב- VAE).
- רקע טוב בהסתברות לא יזיק 🙂
מבוא:
מודלים גנרטיביים מבוססי רשתות נוירונים ליצירת דאטה ויזואלי רשמו התקדמות מרשימה בשנים האחרונות. מודלים כמו StyleGAN2 ו- VQ-VAE2 מסוגלים לגנרט תמונות מגוונות באיכות מרשימה בדומיינים שונים. כרגע רוב המודלים הגנרטיביים עם תוצאות SOTA הם מסוג גאן ו-VAE (עם יתרון ניכר לגאנים). מלבד גאנים ו- VAEs קיימים סוגים נוספים של מודלים גנרטיביים שמבוססים על גישות אחרות כמו מודלים דיפוזיאוניים ומודלים מבוססי זרימה (flow). עד כה מודלים אלו לא הצליחו (לפחות מבחינת המדדים המקובלים כמו FID ו-Inception Score – IS) להציג ביצועים ברי השוואה עם תוצאות SOTA. נציין כי לפחות מבחינה ויזואלית איכות התמונות הנוצרות באמצעות מודלים דיפוזיוניים ומבוססי זרימה לא נופלת מזו של אלו הנוצרות באמצעות גאנים ו-VAE-ים המתקדמים ביותר (דעה אישית).
המאמר הנסקר הוא הראשון (למיטב ידיעתי) שבו הצליח מודל דיפוזיאני להגיע לביצועים טובים יותר ממודלים גנרטיביים, אשר נותנים כיום את התוצאות הטובות ביותר. זו בשורה משמעותית עד כדי כך שמחברי המאמר ציינו אותה ישירות בכותרת 🙂
תמצית מאמר:
המאמר הנסקר מתבסס על שני מאמרים קודמים ומציע שורת שיפורים שהצליחו ״להרים את הביצועים של DDPM" לרמה של גאנים ומעבר לכך:
- מאמר רקע 1 למעשה הציע את מה שנקרא Denoising Diffusion Probabilistic Model או בקיצור DDPM. מעניין כי מודלים דיפוזיאוניים לגנרוט דאטה הומצאו עוד ב-2015 ב- מאמר רקע 0.
- מאמר רקע 2 הציע רפרמטריזציה של פונקציית הלוס, שינוי של תהליך האימון (יפורט בהמשך) וכמה טריקים נחמדים נוספים שבפועל שיפרו את איכות התמונות המגונרוטות באמצעות המודל.
- המאמר הנסקר מציע דרך לנצל דאטה מתויג לאימון מודל דיפוזיאוני לצד כמה שיפורי ארכיטקטורה של רשתות נוירונים המעורבות בתהליך הגנרוט.
כאמור, המאמר הנסקר מציג שורת שיפורים למאמר רקע 2 שבעצמו מהווה גרסה משודרגת של מאמר רקע 1. עקב כך אתחיל מסקירה מפורטת ומעמיקה של מודל דיפוזיאוני שהוצג במאמר רקע 1, לאחר מכן אסקור את השדרוגים של מאמר רקע 2 של המאמר הנסקר.
תקציר מאמר רקע 1:
מודל דיפוזיאוני DDPM לגינרוט דאטה: הרעיון של DDPM הוא די פשוט. לוקחים תמונה, מוסיפים אליה רעש גאוסי במשך כמה איטרציות (מאות או אלפים) עד שהתמונה הופכת להיות לרעש גאוסי איזוטרופי (N(0, I – זה נקרא תהליך קדמי (forward process). המטרה של מודל דיפוזיאוני הוא למדל (ללמוד) את התהליך ההפוך (reverse process) – כלומר לגנרט תמונה מרעש גאוסי איזוטרופי צעד אחרי צעד.
מטרת אימון DDPM: המטרה היא למדל את ההתפלגות Pr(xt-1|xt) כאשר xt היא התמונה המתקבלת באיטרציה t של התהליך הקדמי המתואר לעיל. באופן פורמלי, אם נסמן את התפלגות התמונות מהדאטהסט ב- x0~q(x0), אז התהליך הקדמי יתואר באופן הבא:
כאשר (βt ∈(0, 1 הם סדרה של קבועים דטרמיניסטיים ו- T מסמן את מספר האיטרציות של התהליך.
חיזוי: כמו שכנראה כבר ניחשתם זמן החיזוי הוא עקב האכילס של מודלים דיפוזיוניים. כדי לבנות תמונה מרעש אנו צריכים לשחזר את כל הצעדים של התהליך ההפוך. המאמר הנסקר מדבר על בערך 4000 איטרציות המצריכים הרצה של 4K רשתות אחת אחרי השנייה שזה כמובן מאוד בעייתי.
פרטים על הרעש המוסף: תוחלת (פר פיקסל) של רעש גאוסי המוסף בכל איטרציה תלויה בערך של הפיקסל. רעש המוסף עבור פיקסל {i, j} באיטרציה t מוגדר באמצעות התפלגות נורמלית N(√αt xt-1,ij, βt), כאשר. αt=1- βt ו- xt-1,ij הינו ערך הפיקסל {i, j} בתמונה מורעשת מאיטרציה t-1.
נקודה חשובה: מידול של התהליך ההפוך עשוי להיראות פשוט לאור העובדה שהתהליך הקדמי (המתואר באמצעות התפלגות q(xt|xt-1)) מתפלג גאוסית. אולם השערוך של q(xt-1|xt) אינו משימה פשוטה והתפלגות זאת אינה גאוסית. הסיבה לכך היא שלהבדיל מהתהליך הקדמי שהוא הוספה של רעש גאוסי בעל תוחלת ושונות ידועות לתמונה, התהליך ההפוך הוא למעשה ניקוי של תמונה מורעשת מחלק של הרעש שיש בה (מכאן באה המילה denoising בשם של המודל). כדי לבצע denoising כזה נדרשות ״הבנות״ של ההתפלגויות של תמונות המתקבלות בשלבים השונים של תהליך דיפוזיוני.
עקב המורכבות הטמונה במידול של q(xt-1|xt) משערכים אותה באמצעות התפלגות גאוסית פרמטרית p(xt-1|xt) הממודלת ע״י ,מי היה מנחש, רשת נוירונית. פורמלית:
כאן Σθ(xt, t) = γtI (כלומר הרשת חוזה רק את סקלר γt).
נקודה חשובה: למה ניתן לקרב q(xt-1|xt) באמצעות p(xt-1|xt) גאוסי בדיוק טוב?
הרי כבר אמרנו ש- q "טומנת בה ידע על התפלגות התמונות" של הדאטהסט עליו מאומן DDPM. מתברר כי קירוב זה עובד טוב כאשר הרעש המוסף בכל שלב של תהליך קדמי הוא בעל תוחלות ושונויות נמוכות מספיק (אחד מהמאמרי רקע מציין כי קיימת הוכחה של גאוסיות תחת תנאים מסוימים על התפלגות של q(x0) אך לא ראיתי אותה).
DDPM מול מודלים גנרטיביים אחרים: ברמת העיקרון DDPM די דומה למודלים גנרטיביים אחרים כמו גאן, VAE או מודלי זרימה שגם יוצרים תמונה מרעש. אבל כאן הדמיון בין גישות אלו נגמר כי הדרכים בהן הן ממדלות מיפוי מרעש לתמונה הן מאוד שונות (למרות ש-VAE ו-DDPM משתמשים ב-ELBO לבנייה של פונקציית המטרה שלו).
איך מאמנים מודל דיפוזיוני? מטרת האימון של מודל דיפוזיוני היא מיקסום לוג של נראות מירבית (log likelihood) של הדאטהסט ביחס לוקטור פרמטרים θ. כמובן לוג של נראות מירבית של דאטהסט נתון הוא סכום של log(p(x)) עבור כל התמונות x מהדאטהסט. בדומה ל- VAE (אך עם קצת סיבוך עקב איטרציות מרובות המעורבות בתהליך), משתמשים בחסם תחתון (ELBO) כדי לקבל את פונקציית מטרה Lvlb של בעיית אופטימיזציה עבור מודל דיפוזיאוני:
כאן p(xT) הוא רעש גאוסי איזוטרופי.
הסבר על האיברים של Lvlb:
- L1 – מודד עד כמה "סביר" לקבל את התמונה המקורית x0 מתמונה x1 שהתקבלה בשלב לפני האחרון של התהליך ההופכי.
- Lt, 0 < t < T – מודד דמיון בין ההתפלגות המשערכת p(xt-1|xt) לבין ״ההתפלגות האמיתית״q(xt-1|xt, x0) הנדגמת לתמונה x0 מהדאטהסט .
- LT – מודד עד כמה xT, המתקבל בשלב האחרון של התהליך הקדמי', "קרובה" (במונחי התפלגות) לרעש גאוסי איזוטרופי.
תהליך אימון של DDPM בגדול: פונקציית הלוס שלנו היא סכום של T מחוברים אי שליליים. כדי למזער אותה, דוגמים [t ∈ [0, T ומבצעים איטרציה של gradient descent על האיבר Lt של הסכום. כאמור אנו מאמנים רשת Nθ כדי לחזות את התפלגות p(xt-1|xt) לכל [t ∈ [0, T. בכל איטרציה מאפטמים את הפרמטרים של Nθ כדי למזער את הלוס Lt עבור t הנדגם (t מוזן לתוך הרשת).
פלט של הרשת: הדרך הטבעית היא לאמן את הרשת לחזות את μθ(xt, t) ו- Σθ(xt, t) = γtI תוחלת ומטריצת הקווריאנס של p(xt-1|xt) . אך ניתן גם לאמן Nθ לחזות פרמטרים אחרים המעורבים בתהליך (כמו התפלגות p(x0) של התמונה המקורית x0) מהם (יחד עם xt) ניתן לגזור את μθ(xt, t) ו- γt.
הערה: במאמר רקע 1 γt לא נחזה באמצעות רשת נוירונים אלא משתמשים בקירוב שלו – הסיבות לכך יפורטו בהמשך.
מאמר רקע 1 בחר לאמן Nθ כדי לחזות פרמטר אחר שניתן לגזור ממנו את μθ(xt, t) תוך שימוש בתכונות של התהליך הקדמי. כעת נרחיב איך ניתן לעשות זאת. ניתן לבצע את רפרמטריזציה הבאה להתפלגות q:
כאשר ε הוא רעש גאוסי סטנדרטי (N(0,I. אינטואיטיבית די ברור כי xt|x0 מתפלג גאוסית כי x t נבנה מ- x0 באמצעות הוספת רעשים גאוסיים בעלי תוחלות ושונויות ידועות. בנוסף מתקיים:
במאמר רקע 1 מאמנים Nθ לחזות את רעש המוסף ε בשלב t (המחברים טוענים שזה משפר את איכות התמונות המיוצרות) שממנו ניתן לגזור μθ(xt, t) באופן הבא:
למעשה פונקציית לוס שהרשת Nθ מאומנת למזער היא:
הערה: כמו שכבר ציינתי מאמר רקע 1 לא משערך γt אלא משתמש רק בקירובו t (שונות של xt|xt-1). למעשה ניתן לראות כי β˜t < γt < βt (ערכים דטרמיניסטיים) אך בפועל שימוש בכל אחד חסמים אלו הוביל לתוצאות מאוד דומות. צריך לציין שימוש ב- Lsimple שקול למשקול של המחוברים בפונקצית המטרה המקורית Lvlb (זה נובע מהצורה של מרחק KL בין התפלגויות גאוסיות).
ארכיטקטורת רשת:
מבוססת על זו של PixelCNN++ שהיא שילוב U-Net ו- Wide ResNet. כדי לקודד את מספר איטרציה t משתמשים בקידוד מיקומי (positional encoding) מהמאמר המקורי על הטרמספורמרים (Attention is All You Need, זוכרים?). המחברים גם משתמשים במנגנון self-attention בין שכבות קונבולוציה ברזולוציות שונות.
בכך סיימנו לתאר את DDPM כמו שהוצג במאמר רקע 1. כעת נעבור לשינויים שהוצעו למודל זה במאמר רקע 2 ובמאמר הנסקר.
תקציר שיפורים/שינויים של DDPM:
למעשה יש ארבעה סוגים של שיפורים שבזכותם DDPM הצליח להכות את הגאנים:
שינויים בפרמטרים של התהליך הקדמי:
- מאמר רקע 2 (פרק 3.2): קבועי [βt, t ∈ [0, T נקבעים באופן שונה. המחברים שמו לב כי השלבים האחרונים של התהליך הקדמי יוצרים תמונות רועשות מדי ולא תורמים לאיכות התמונה המגונרטת. עקב כך הוצע לקבוע קבועים אלו כדי "להאט הפיכתה של תמונה לרעש".
שינויים בפונקציית לוס ובתהליך אימון של Nθ :
- מאמר רקע 2 (פרק 3.1): כאמור בגרסה המקורית של DDPM המחברים החליטו לא לשערך שונות γt של xt-1|xt והסתפקו בשערוך של תוחלתו (באופן עקיף דרך ε ). ההסבר שלהם לגבי למה זה עובד מספיק טוב היה טמון בעובדה כי β˜t < γt < βt אך βt ו- β˜t הם מאוד קרובים עבור רוב ערכי t. מאמר רקע 2 נקט בגישה אחרת והציע רפרמטריזציה קמורה של (γt=exp(vlog(β˜t ) + (1-v) logβt, כאשר v ∈ (0,1) ואימנו רשת לשערוך של v. נציין כי פונקצית הלוס הקודמת Lsimple לא מכילה את t אז המחברים השתמשו צירוף לינארי של Lsimple ו- Lvlb בתור פונקציית לוס חדשה.
- מאמר רקע 2 (פרק 3.3) מחליף דגימה יוניפורמית ב- t ב- importance sampling. ההסתברות של בחירת ערך t פרופורציאונלית לערך שגיאת Lt הממוצע. לטענת המחברים זה מקטין את התנודתיות של הגרדיאנטים שלהם.
- המאמר הנסקר משתמש בדאטה מתויג לאימון של DDPM. הרעיון הוא לנצל תמונות מתויגות ל״ניווט של מודל דיפוזיוני לכיוון״ שבו תמונות שהוא מייצר בתהליך הופכי, יסווגו עם הקטגוריה נכונה בוודאות גבוהה באמצעות מסווג מאומן מראש. כלומר לכל ערך של t מאמנים רשת מסווגת Nφ,t שהפלט שלה עבור תמונה xt (מאיטרציה t) הוא pφ(y|xt) עבור קטגוריה y. במהלך האימון לתמונה בעלת קטגוריה y, ״מתקנים״ את ההתפלגות xt-1|xt באופן כזה שהתמונות תקבלנה ערך גבוה של pφ(y|xt-1). במקום לשערך p(xt-1|xt) אנו משערכים (דוגמים מ-): p,(xt-1|xt,y)=Zp(xt-1|xt)p(y|xt-1). כמו שאתם יכולים לנחש שערוך כזה לא לגמרי קל ומערב מתמטיקה לא טריוויאלית (זה מבוסס על score-based generative models הקשורים לדינמיקה של לנגבין). יותר פרטים נמצאים בפרק 4 של המאמר הנסקר.
שיפורים בארכיטקטורה של Nθ:
- מנגנון attention בעל רזולוציות מרובות (multi-resolution).
- שימוש בבלוקים residual של BigGAN ל- up/downsampling.
- (Adaptive group normalization (AdaGN
זירוז תהליך החיזוי: שינוי בהגדרת תהליך הופכי שמאפשר חיזוי מדויק של xt-1 מ- xt-1+m עבור m>0. שינוי זה מאפשר לדגום את xt כל m צעדים ול-m גדול מקטין את זמן החיזוי באופן משמעותי. המתמטיקה העומדת מאחורי ההגדרה החדשה הזו די לא טריוויאלית ובנוסף התהליך הקדמי מאבד את המרקוביות שלו כי xt תלוי באופן מפורש גם ב-x0.
הישגי מאמר:
כאמור המודל הדיפוזיאוני המוצע הצליח להכות את הגאנים המובילים מבחינת FID. זמן החיזוי עדיין נותר די גבוה יחסית לגאן אבל יש שיפור ניכר יחסית למודלים דיפוזיאוניים קודמים.
נ.ב.
מאמר ממש מגניב המצריך הבנה מעמיקה של 3 מאמרים שקדמו לו בנושא של מודלים דיפוזיוניים (ועוד שניים בנושאים סמוכים). המתמטיקה לא טריוויאלית אבל היה שווה את המאמץ.
#deepnightlearners
הפוסט נכתב על ידי מיכאל (מייק) ארליכסון, PhD, Michael Erlihson.
מיכאל עובד בחברת הסייבר Salt Security בתור Principal Data Scientist. מיכאל חוקר ופועל בתחום הלמידה העמוקה, ולצד זאת מרצה ומנגיש את החומרים המדעיים לקהל הרחב.