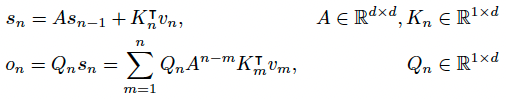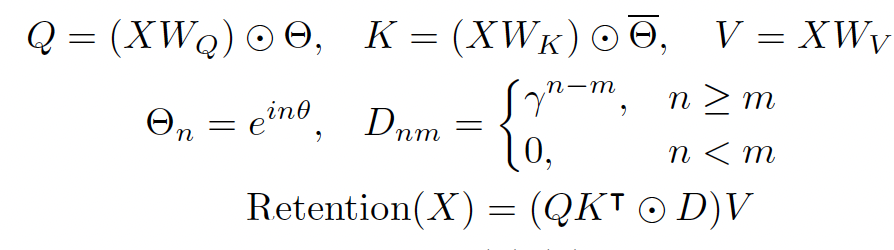Hyena Hierarchy: Towards Larger Convolutional Language Models

היום סוקרים את המאמר השביעי בסדרה וכאן אני חייב להודות שלקח לי הרבה מאוד זמן לצלול למאמר הזה לעומק למרות שטכנית המאמר לא מורכב במיוחד (בטח לא קרוב ל Hippo). אבל המאמר כתוב בצורה נוראית: מצד אחד הוא עמוס בפרטים לא מהותיים ומצד שני נעשה מאמץ ניכר (על ידי המחברים) להסתיר את הפרטים המהותיים עם מלל אינסופי. לא יודע האם זה נעשה בזדון או לא אבל המאמר הזה לקח לי בערך פי 4 יותר זמן ממאמר ממוצע שזה הרבה סטיות תקן מהממוצע (יש לי מדגם די גדול).

אחרי ששחררתי את הקיטור אפשר להתחיל לסקור את המאמר זה שמציע הכללה חמודה ל H3 שסקרנו קודם. H3 היה די נחמד אבל עדיין הביצועים שלו לא היו בשמיים עבור כמה משימות על הדאטה בעלי אורך הקשר ארוך מאוד. אז באו לנו מחברי Hyena והציעו לשפר את ביצועי H3 אך לא במחיר של עלייה ניכרת במשאבי חישוב והזיכרון.

אוקיי, אז מה הם הציעו בעצם? אתם זוכרים שב-H3 אנו לקחנו וקטורי מפתח עבור הטוקנים בתוך חלון ההקשר (=מטריצה K) העברנו אותם דרך SSM (State-Space Models) ואז הכפלנו אותם בווקטורי שאילתה (=מטריצה Q) והעברנו את התוצאה דרך SSM נוסף עם מטריצה A אחרת ואת התוצאה הכפלנו בווקטורי ערך עבור כל הטוקנים בתוך חלון ההקשר (=מטריצה V)? כל המנגנון הזה הוא למעשה attention לינארי.

אז ההכללה הראשונה המוצעת במאמר היא הגדלת מספר הוקטורים שעליהם מופעלת SSM (בצורה לא מפורשת – נדבר על זה עוד מעט) ל N. כלומר יש לנו 1+N הטלות של ייצוג הטוקנים (אחת עבור מטריצת הערך V). אחרי שיש לנו את ההטלות האלו מפעילים עליהם מה שבמאמר נקרא Short Convolution (קונבולוציה קצרה) בציר הטוקנים. זה נעשה כנראה כדי ללמוד את האינטראקציות בין הטוקנים הסמוכים (המאמר לא מסביר כלום לגבי זה).

מפה העניינים קצת מסתבכים. אנו לוקחים מטריצת הערך V מההטלה האחרונה ומפעילים עליהם SSM (אותה מערכת דינמית לינארית) אבל בצורה לא מפורשת. מה זה אומר אבל? אנו יודעים שהפעלת SSM לסדרה של L טוקנים שקולה להפעלה של קרנל קונבולוציה באורך L על ייצוגי טוקנים אלו. קרנל קונבולוציה זה מוגדר על ידי המטריצות המגדירות את ה-SSM (שזה A, B, C). אז ניתן להגדיר SSM בצורה לא מפורשת דרך הקרנל הזה. צריך לזכור פעולה זו שקולה להכפלת וקטורים, המרכיבים מטריצת ערך V, במטריצת קונבולוציה גדולה (= שזה אותו מנגנון של attention לינארי).

למשל ב-H3 (שסקרנו בפעם הקודמת) היו לנו שני SSMs (עם מטריצה אלכסונית ועם מטריצת הזזה ב-1) ומתברר שניתן לייצג אותם בצורה לא מפורשת עם קרנל שהוא מכפלה של שתי מטריצות שכל אחת מהן היא מכפלה של מטריצה אלכסונית במטריצת Toeplitz. מה שמיוחד במטריצת Toeplitz היא שכל שורה בה כי הזזה שמאלה של השורה הקודמת. תכונה מעניינת של כל מטריצה Toeplitz היא שהיא מהווה ייצוג של קרנל קונבולוציה.

אז המחברים לקחו את הייצוג הלא מפורש של SSM ובנו אותו מ- N מכפלות של מטריצות אלכסוניות ומטריצות Toeplitz (שונות). כלומר מתחילים מטריצה V עבור הטוקנים מפעילים עליה מיפוי $H$  לינארי (= קרנל קונבולוציה) די מסורבל. כלומר H הוא הרכבה של N מיפויים $H_i, i=1,…N$ לינאריים שכל אחת מהן היא קונבולוציה המיוצגת על ידי מטריצה Toeplitz (מס' i) ומכפלת התוצאה איבר-איבר בהטלה מספר i של וקטורי הטוקנים. במאמר כל הסיפור הזה נקרא Hyena operator מסדר N.

אוקיי, מה הבעיה העיקרית עם הגישה הזה? זה דורש הרבה זיכרון בטח עבור N גדול יחסית. אז המאמר מציע פתרון מאוד אלגנטי. במקום ללמוד את כל N קרנלים אלו בצורה מפורשת נגדיר אותם באמצעות רשת נוירונים רדודה (fully-connected). גם נוכל לשלוט על מספר פרמטרים וכך לשמור על זיכרון קבוע פחות או יותר לכל ערך של N. כך ניצור את כל N קרנלים עם רשת אחת בלבד. ארכיטקטורת רשת רדודה זאת היא די מיוחדת והיא מכילה פונקציות אקטיבציה מחזוריות (כדי ליצור קונבולוציות עם תדרים גבוהים).

בנוסף מכפילים קרנל זה (איבר איבר) בפונקציה מעריכית עם פרמטר חיובי דלטה $\exp(-\delta t)$ בציר הטוקנים. הכפלה זו באה לשקף דעיכה בהתחבשות בטוקנים(=attention) ככל המרחק בינם לבין הטוקן החזוי יורד. המאמר משתמש בכמה אופרטורי Hyena (ערוצים) במקביל עם מקדמי $\delta$ שונים המבטאים קצבי דעיכה שונים של attention. כל אופרטור כזה מופעל על וקטורי קידוד מיקומי (positional encoding).

ודבר אחרון: כל הקונבולוציות מחושבות דרך FFT(Fast Fourier Transform) וגם IFFT כמו במאמר של H3 (כי זה פשוט יותר מהיר מצריך פחות זיכרון). כמובן כל SSM (גם לא מפורש) מופעל על כל מימד של ייצוג הטוקנים שטיפה מסבך את התיאור אבל עדיין הכל נשאר לינארי.

RWKV: Reinventing RNNs for the Transformer Era

https://arxiv.org/abs/2305.13048

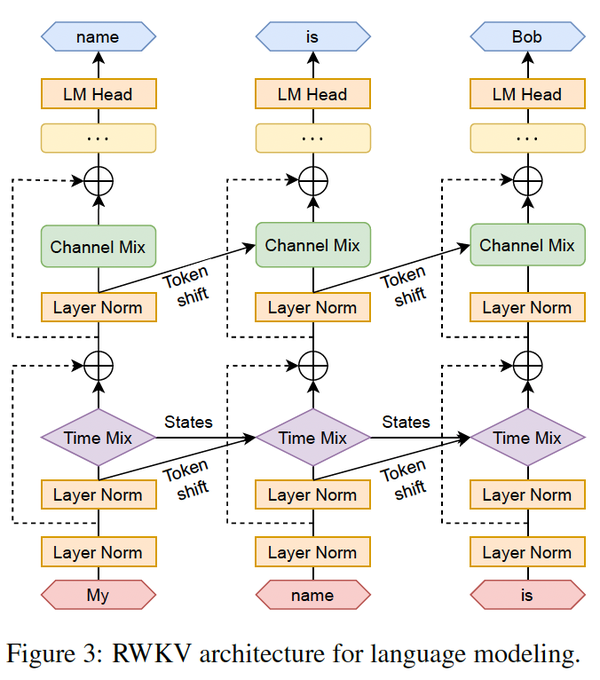
אחרי כמה מאמרים כבדים הפעם יש לנו מאמר קליל יחסית. אתם אולי זוכרים שהמאמר השלישי שסקרנו בסדרה (״Transformers are RNNs: Fast Autoregressive Transformers with Linear Attention״) הראה שטרנספורמר עם attention לינארי ניתן לייצג בתור RNN מצד אחד (כלומר ניתן להפעלה באופן איטרטיבי כאשר הוא דוחס את הטוקנים הקודמים בוקטור זיכרון אחד) ומצד שני ניתן להפעלה באופן כמו הטרנספורמר מן המניין. כלומר יש בו את הדואליות שרצינו: חיזוי מקבילי של טוקנים ממוסכים במהלך האימון וחיזוי טוקנים בעל סיבוכיות לינארית במהלך ההיסק (=inference).

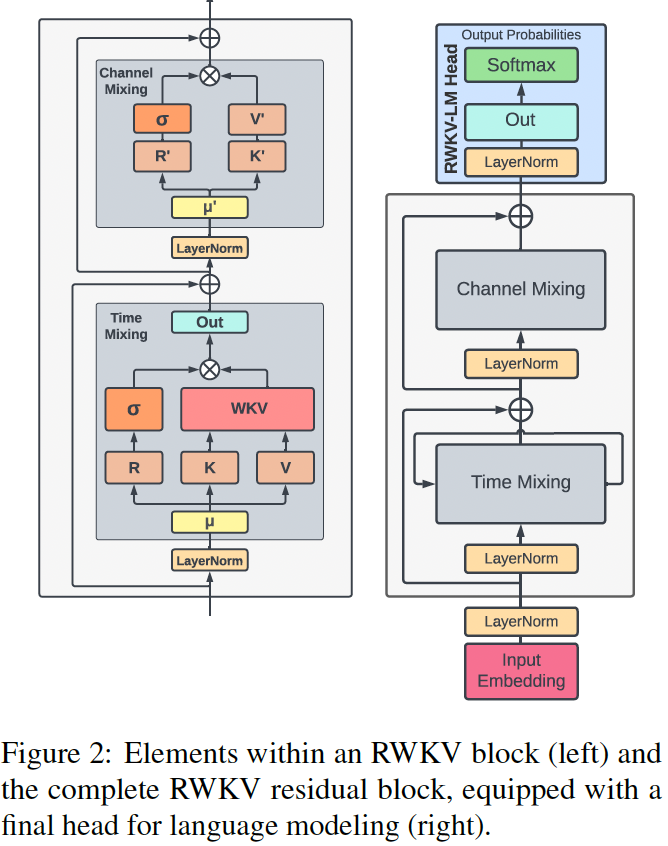
המאמר שנסקור היום מקרב את הטרנספורמר ו-RNN באופן מפורש אפילו קצת יותר. המחברים לוקחים טרנספורמר עם מנגנון ״attention״ ״פשוט יותר״ ומוסיפים קצת RNN לאופן בו מחושבים מטריצות מפתח K ומטריצת ערך V. אבל קודם אספק לכם כמה פרטים על מנגנון "attention" שלקחו המחברים בתור בסיס ולמה אני שם אותו כאן בגרשיים. אז מנגנון הזה נלקח מהמאמר AFT) An Attention Free Transformer) שלפי שמו נראה שהמאמר מציע טרנספורמר ללא attention כלל!

אוקי, אז מה הסיפור של AFT ומה זה בכלל טרנספורמר ללא attention (לי זה נשמע על ההתחלה כמו אוטו ללא מנוע). AFT מחליף את המנגנון הרגיל של חישוב attention של הטרנספורמר בכזה שדורש משמעותית פחות זיכרון מהטרנספורמר הרגיל (בגרסתו הפשוטה גם סיבוכיות חישובית מוקטנת עד כדי לינארית במונחי אורך הקלט) ועושה את זה בדרך מאוד הגיונית. מנגנון AFT מחליף את המכפלות הפנימיות בין וקטור שאילתה $q_i$ ווקטור המפתח $k_j$ באקספוננט של סופטמקס (שזה הלב של המנגנון והסיבה לסיבוכיות הריבועיות) בסכום של וקטורי המפתח עם מטריצת משקלים נלמדת $w_{ij}$ (מנורמל). כלומר לא מתחשבים בוקטורי שאילתה $q_i$ אלא משתמשים במקדמים קבועים ומחושבים על סמך סט האימון.

לאחר מכן בונים צירוף לינארי עם וקטור הערך $v$ כמו בטרנספורמר הרגיל. כלומר מקדמי ה-attention בין טוקן i לטוקן j לא תלויים באופן מפורש בייצוג טוקן i אלא רק ב- i ו-j. בחירות חכמות(פרמטריזציה) של $w_{ij}$ מאפשרות להקטין את דרישות זיכרון והסיבוכיות החישובים כאשר המחיר הוא כמובן expressiveness של המודל. אחת הבחירות של $w_{ij}$ היא פונקצית דועכת. מעריכית כאשר הארגומנט הוא מרחק בין הטוקנים (המאמר המסוקר משתמש בה).

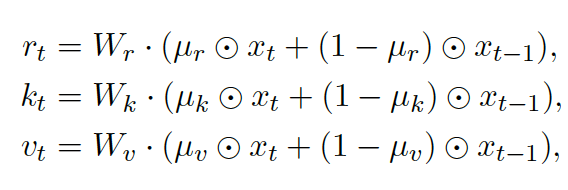אוקיי, אז איך מלבישים על זה RNN? לוקחים את המנגנון ה- attention מהפסקה הקודמת עם שפצור קל ליציבות נומרית – הוספה של וקטור u (המנגנון הנקרא wkv) ומפעילים אותו עם וקטורי מפתח וערך $K$ ו- $V$ מחושבים כמו ב-RNN. כלומר בונים וקטורים אלו ($K$ ו- $V$) תלוים באופן מפורש בייצוג הטוקן הנוכחי וגם בייצוג הטוקן הקודם(זה כל הקטע). במקום להכפיל את ייצוג הטוקן במטריצות $W_k$ ו- $W_v$ (כמו בטרנספומר הרגיל) מכפילים אותם בסכום ממושקל (עם משקלים נלמדים) של ייצוג הטוקן $x_t$ הנוכחי וייצוג בטוקן הקודם $x_{t-1}$.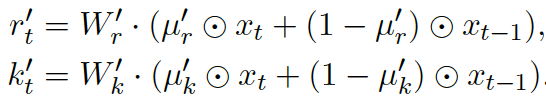

בנוסף מחשבים וקטורי r (הנקרא receptance) באותה הצורה (עם $x_t, x_{t-1}$ ומטריצת $W_r$). וקטורי r למעשה משמשים לנו כדי ״לשערך״ עד כמה אנו צריכים להתחשב בה (מחושבת עם הסיגמואיד כמו בזמנים הטובים ב-RNN). כל הסיפור הזה נקרא באופן לא מפתיע rwkv. בסוף משלבים את התוצאה של rwkv עם וקטורי מפתח וערך המחושבים באותה צורה כמו ב-rwkv (התחשבות ב- $x_t$ ו- $x_{t-1}$). אבל עם מטריצות הטלה נלמדות אחרות). איך משלבים? כרגיל בצורה של ResNet. וזהו זה.

שמח לבשר שהמאמר הבא שנסקור בדרך לממבה גם יהיה קליל (Retentive Network).

Retentive Network: A Successor to Transformer for Large Language Models

https://arxiv.org/abs/2307.08621

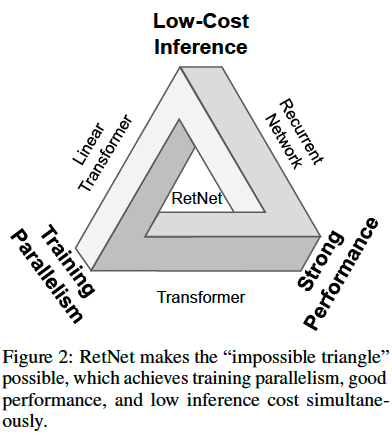
זה הולכת להיות הסקירה הקלה ביותר (אך קצת ארוכה). המאמר משתמש באופן די אלגנטי ברעיונות שהוצע ב 8 המאמרים שכבר סקרנו. אזכיר שהמכנה המשותף במאמרים שסקרנו היתה מטרה למצוא ארכיטקטורה בעלת דואליות הבאה:

• ניתנת לאימון באופן מקבילי כמו הטרנספורמרים
• היסק (inference) מהיר (=לינארי במונחי אורך חלון הקשר) שלא מצריך התחשבות מפורשת בכל טוקני של חלון ההקשר

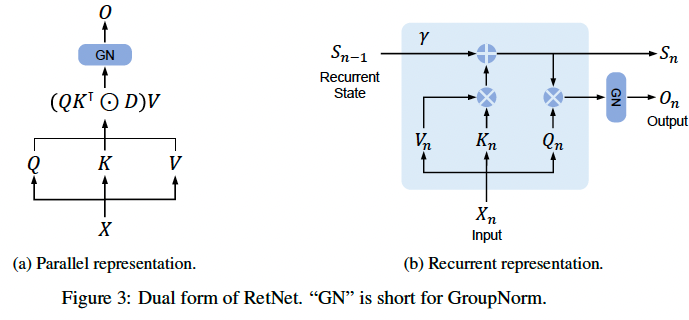
הארכיטקטורה שהמאמר מציע היא אכן מבורכת בדואליות זאת ובאותו הזמן היא מאוד פשוטה וקלה להסבר (ככה נראה לי). אתם בטח זוכרים את הייצוג הקונבולוציוני של (SSM (state-space model עבור ייצוג הזיכרון של סדרת טוקנים? אם לא אזכיר בקצרה. עבור סדרת טוקנים נתונה יש לנו מערכת דינמית לינארית (DMS) שבאמצעותה אנו מייצגים בצורה איטרטיבית את זיכרון $s_n$ הנצבר ב n הטוקנים הראשונים בסדרה. בעזרת DMS ניתן לחשב את $s_n$ מייצוג הזיכרון קודם $s_{n-1}$ ומייצוג של טוקן ה-n, מסומן $v_n$. לאחר מכן באמצעות וקטור $s_n$ אנו ממדלים פלט המודל $o_n$ עבור טוקן n (= ייצוג תלוי הקשר או contextualized embedding של טוקן n) דרך הטלתו עם מטריצה $Q$.

נציין כי DMS מגדירה את מעבר(הלינארי) בין ייצוג של הזיכרונות n-1 ו-n מאפשר חיזוי במקבילי עבור כמה טוקנים במהלך אימון. אותה DMS מוגדרת באמצעות מטריצות A ו-K וכאמור הפלט $o_n$ מוגדר באמצעות מטריצה הטלה $Q$. מטריצות $Q$ ו- $K$ הן אלו שנקראות בטרנספורמר מטריצות שאילתה וערך ומחושבות באותה צורה: $Q = XW_Q, K = XW_K$, כאשר X הוא ייצוגי הטוקנים. עכשיו השאלה איך אנו מגדירים חישוב מקבילי של $o_n$ עבור כמה n? הרי עבור n גדול מספיק העלאה של מטריצה $A$ בחזקה עלולה להיות יקרה גם מבחינת זיכרון וגם במבחינת מאשבי חישוב. אז פותחים אחד הפרקים הראשונים של ספר של אלגברה לינארית ומגלים שניתן לתאר מטריצות ריבועיות (לא כולן!) בתור $A=LDL^{-1}$ כאשר $D$ היא אלכסונית עם ערכים מרוכבים $\lambda_j\exp(i\theta_j), j=1,….,d$. מה בעצם טוב בייצוג הנחמד הזה? זה מאפשר לנו להעלות את מטריצה $A$ בחזקה והבעיה שלנו עם חישוב $A^n$ נראית פתורה. המאמר גם מניח ש $\lambda_j ==\lambda, j=1,..,d$. וזה מאפשר את ייצוג פשוט של המודל שהם מציעים למעשה המחברים מחליפים את מנגנון ה-attention הממומש עם סופטמקס בטרנספורמרים עם ה-attention הדועך בצורה מעריכית כפונקציה של בין הטוקנים. חדי העין שקראו את הסקירה הקודמת שלי ישימו לב שעיקרון דומה ממומש גם ב-RWKV אבל די מיצוע מעריכי של המידע מהטוקן הקודם.

וכמובן ייצוג כזה חישוב מהיר עבור כל טוקן במהלך היסק (שזה תכונה 2 שלנו). המאמר מציע שני שכלולים נחמדים ל-RetNet. הראשון הוא כדי להאיץ את מהירות האימון עוד יותר ולנצל את משאבי החישוב הזמינים ניתן לחלק את הטוקן לצ'אנקים ולהפעיל חישוב מקבילי בתוך כל צ'אנק וחישוב איטרטיבי בין צ'אנקים. שכלול נוסף הוא שימוש במקדמי $\lambda$ שונים ל״ראשים״ (heads) שונים של RetNet. זה למעשה מקנה למודל יכולת יותר להתמקד בטוקנים קרובים יותר ($\lambda$ גבוה) ו״לפזר״ את ה-attention גם טוקנים רחוקים ($\lambda$ נמוך). שילוב של ראשים בעלי lambdas שונים ״לחקות״ את הטרנספורמר (לפחות במידה מסוימת).