Removing Bias in Multi-modal Classifiers: Regularization by Maximizing Functional Entropies (סקירה)

סקירה זו היא חלק מפינה קבועה בה אני סוקר מאמרים חשובים בתחום ה-ML/DL, וכותב גרסה פשוטה וברורה יותר שלהם בעברית. במידה ותרצו לקרוא את המאמרים הנוספים שסיכמתי, אתם מוזמנים לבדוק את העמוד שמרכז אותם תחת השם deepnightlearners.
לילה טוב חברים, היום אנחנו שוב בפינתנו deepnightlearners עם סקירה של מאמר בתחום הלמידה העמוקה. היום בחרתי לסקירה את המאמר שנקרא:
Removing Bias in Multi-modal Classifiers: Regularization by Maximizing Functional Entropies
פינת הסוקר:
המלצת קריאה ממייק: מומלץ מאוד אך לא חובה (זהירות: מתמטיקה קצת קשוחה בפנים).
בהירות כתיבה: גבוהה.
רמת היכרות עם כלים מתמטיים וטכניקות של ML/DL הנדרשים להבנת מאמר: נדרשת רקע מוצק בתורת האינפורמציה וכלים מאנליזה פונקציונלית בנוסף להבנה עמוקה בסוגיות העולות באימון של מודלים מולטימודליים.
יישומים פרקטיים אפשריים: שיפור ביצועים באימון מסווגים לבעיות מולטימודליות עם חוסר איזון בין מודים שונים.
פרטי מאמר:
לינק למאמר: זמין להורדה.
לינק לקוד: זמין כאן.
פורסם בתאריך: 21.10.20, בארקיב.
הוצג בכנס: NeurIPS 2020.
תחומי מאמר:
- מסווגים לבעיות מולטימודליות.
- שיטות רגולריזציה.
כלים מתמטיים, מושגים וסימונים:
- אנטרופיה פונקציונלית (FE).
- אינפורמצית פישר פונקציונלית.
- אי שוויונות לוגו של סובולב ושל פואנקרה.
- טנזוריזציה במרחבי הסתברות מכפליים (product probability spaces).
תמצית מאמר:
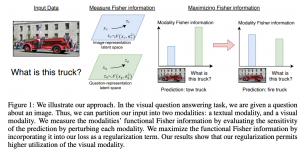
המאמר מציע שיטה להתמודד עם הסטייה בכיוון של תת-קבוצה של מודים בתהליך אימון על בעיות סיווג מולטימודליות. כאשר זה קורה המסווג עלול להיות מוטה כלפי תת-קבוצה של המודים ולהתעלם (להתחשב פחות) מהמודים האחרים. למשל ניקח לדוגמא דאטה סט הנקרא Colored MNIST שסט האימון וסט הוולידציה שלו מכילים תמונות צבעוניות של הספרות, והטסט סט מכיל תמונות בגווני אפור. אם מאמנים רשת נוירונים עם לוס רגיל במטרה לסווג את הספרה, ביצועיה (דיוק) על הטסט סט סופגים ירידה משמעותית יחסית לביצועים על סט האימון ועל סט הוולידציה. הסיבה לכך היא שהמסווג למד להתחשב בעיקר בצבע של תמונה (המוד הראשון) ומתעלם לרוב מהצורה של הספרה (המוד השני). עוד דוגמא לכך, היא משימת ״מענה על שאלות ויזואליות״ (מולטימודלית בצורה אינהרנטית), כאשר המסווג עלול לבחור להתמקד רק במציאת תשובה ״הגיונית״ לשאלה ויתעלם מהאינפורמציה הויזואלית . בשביל להתמודד עם סוגייה זו המחברים מציעים להוסיף לפונקציית לוס איבר שמנסה ״להכריח כל מוד לתרום״ לסיווג הסופי. איבר זה מבוסס על אנטרופיה פונקציונלית (FE), שבעזרתה ניתן לאמוד את התרומה של כל מוד לתוצאה של המסווג.
במילים אחרות FE משערכת את "מידת השתנות הממוצעת של התפלגות הפלט של המסווג עבור פרטורבציות (הרעשה) של הקלט״ (במרחבי הייצוג ולא במרחבים המקוריים!!) תחת התפלגות מסוימת על הפרטורבציות (המאמר משתמש בהתפלגות גאוסית באופן טבעי). ככל שמידת השתנות זו קטנה יותר עבור סיווג נתון (כלומר התפלגות של פלט המסווג איננה משתנה בהרבה עבור נקודות בסביבה יחסית רחוקה של הקלט – במרחב הייצוג), המסווג נוטה ״לא לנצל מידע על לפחות חלק מהמודים באופן מיטבי״.
בנוסף מכיוון FE קשורה לשונות של מידת השתנות של התפלגות הפלט, המאמר מציע להוסיף את איבר המשערך שונות זו במקום האיבר של FE. למעשה, ככל שהשונות של מידת ההשתנות קטנה יותר, התפלגות הפלט פחות תלויה בקלט שזה כמובן לא רצוי. מעניין שאיבר רגולריזציה בצורה של שונות משיג שיפור מסוים בביצועים עבור כמה משימות.
רעיון בסיסי:
הרעיון הבסיסי של המאמר הוא להוסיף איבר המשערך FE לפונקציית לוס רגילה (קרוס-אנטרופי). מידת ההשתנות של פלט המסווג עבור פרטורבציות (הרעשה) של דוגמא נתונה מוגדרת במאמר בתור קרוס אנטרופי בינה לבין התפלגויות הפלט שלה (הקלט הנקי והקלט מורעש).
תקציר מאמר:
הבעיה העיקרית עם באנטרופיה הפונקציונלית נעוצה בעובדה שלא ניתן לחשב אותה באופן ישיר, אלא רק באמצעות דגימות של האינטגרנד. בנוסף לכך, FE מכילה איבר לוג של אינטגרל התוחלת ששיערוכו עי״ דגימות עלול להיות מאוד לא מדויק.
אינפורמצית פישר פונקציונלית: המאמר מציע להשתמש בחסם מלעיל ל- FE (הנובע מאי שוויונות לוג של סובולב) עי״ אינפורמצית פישר פונקציונלית (FFI), המהווה הכללה של אינפורמצית פישר קלאסית. כמו שאתם אולי זוכרים, אינפורמצית פישר רגילה (FI) מודדת עד כמה מידע יש בדגימות של משתנה מקרי X המפולג עם פונקצית התפלגות f התלויה בפרמטר t, על הפרמטר הזה. FI מוגדרת בתור תוחלת לפי f של הנגזרת הרביעית לפי t של הלוג של f. עבור ערך פרמטר נתון FI משערכת את ״מידת הקשר״ בין ערכו של הפרמטר לבין הדגימות של המשתנה המקרים X. כלומר ככל ש- FI יותר גבוה ניתן לשערך את בפרמטר ביותר דיוק (אפשר להסיק זאת גם מאי השוויון של ראו-קרמר – הדיוק נמדד שם עי״ שגיאת שערוך ריבועית הממוצעת).
אז ההכללה של FFI מתבטאת בכך שמכפילים את האינטגרנד בפונקציית התפלגות נוספת (במקרה שלנו זה פונקצית התפלגות על הפרטורבציות של נקודות הדאטה (f_per(z) . זה מאפשר להחליף את פונקצית הצפיפות f המופיעה בביטוי המקורי של FI בכל פונקציה אי שלילית (במקרה שלנו הפונקציה הזו היא קרוס-אנטרופי בין התפלגויות של הפלטים (f_ce(z). בדומה ל FFI ,FI גם משערך את מידת ההשתנות של (f_ce(z כאשר הפרמטר שלה z מתפלג עם (f_per(z.
חסם לוג של סובולב על FFI: חסם סובולב מאפשר לחסום את FE מלמעלה ע״י האינטגרל המכיל מנה שהמונה בו הינו נורמה של הגרדיאנט הריבועי של קרוס-אנטרופי (C(z בין התפלגויות של הפלטים (f_ce(z כאשר המכנה הוא (C(z עצמו. שניהם ניתנים לחישוב בצורה מפורשת וניתן להכניסם כמו שהם לפונקצית לוס.
טנזוריזציה של FE לבעיות מולטימודליות: המאמר מציין שנקודה במרחב הלטנטי של במשימה מולטימודליות עשויה להיות מורכבת מכמה מודליות מהמרחבים הלטנטיים השונים. למשל במקרה של משימת מענה על שאלות ויזואליות, המרחב הלטנטי הוא בעצם מרחב פרודקט של שלושה מרחבים: ייצוג התמונה, ייצוג השאלה וייצוג התשובה. המאמר מראה שבמקרים כאלו ניתן לתאר את FE של נקודת דאטה בתור הסכום של האיברים שכל אחד מהם זה FE הממוצע של כל מוד z_i, כאשר הממוצע המחושב על מרחב הפרודקט של שאר המודים (פרט ל i) עם פונקציות התפלגות המורכבת ממכפלה של (f_per(z_j (פרט ל i). ייצוג זה נקרא טנזוריזציה והוא מאפשר לחשב חסם על FI של נקודת דאטה בצורה יחסית קלה. כרגע יש לנו את כל הכלים בשביל לתאר את המבנה של פונקצית לוס המוצעת. לפני שנעבור לתיאור של פונקצית הלוס נדון קצרות בצורה השנייה של איבר רגולריזציה המוצע במאמר קרי שונות של (f_ce(z תחת (f_per(z.
איבר רגולריזציה בצורה של שונות של (f_ce(z: ראשית, המאמר מציין שקיים קשר בין FFI לשונות של (f_ce(z כאשר תקף עבור ערכים קטנים של (f_ce(z. באופן אינטואיטיבי ככל ש FFI של פונקצית (g(z יותר גבוה אז השונות נוטה להיות גבוהה יותר כי שניהם מתארים את מידת השתנות של (g(z תחת אותה מידת הסתברות. בדומה ל FFI גם השונות לא ניתנת לחישוב בצורה מפורשת (רק עי״ דגימות) ואז המאמר משתמש באי שוויון פואנקרה בשביל להקל על החישוב. לבסוף מבצעים טנזוריזציה של הביטוי המתקבל (משתמשים במשפט אפרון-שטרן) כדי לקבל את הביוי הסופי.
מבנה של פונקצית לוס: מכיוון שהמטרה שלנו היא למקסם את FFI, איבר רגולריזציה המתווסף לפונקציה לוס מכיל את ההופכית של החסם על FFI (או שונות) ומחברים אותו ללוס קרוס-אנטרופי סטנדרטי. זה כל הסיפור ואפשר להתחיל את האימון.
הישגי מאמר:
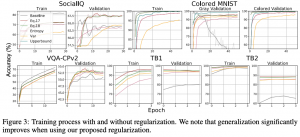
המאמר מדווח על השיפור בדיוק על 4 דאטה סטים מולטימודליים מול כמה גישות עדכניות.
דאטהסטים:
- Dogs and Cats .
- (הבנת מצבים בוידאו) SocialIQ.
- (מענה על שאלות ויזואליות) Colored MNIST.
- VQA-CPv2.
נ.ב.
הרעיון של המאמר די מגניב, לקח לי זמן להבין אותו כי המתמטיקה במאמר די קשוחה. מצפה לראות שימושים של טכניקה זו למגוון רחב של בעיות מולטימודליות (למשל בלמידת באמצעות חיזוקים עמוקה).
#deepnightlearners
הפוסט נכתב על ידי מיכאל (מייק) ארליכסון, PhD, Michael Erlihson.
מיכאל עובד בחברת סייבר Salt Security בתור Principal Data Scientist. מיכאל חוקר ופועל בתחום הלמידה העמוקה, ולצד זאת מרצה ומנגיש את החומרים המדעיים לקהל הרחב.