CoMatch: Semi-supervised Learning with Contrastive Graph Regularization (סקירה)

סקירה זו היא חלק מפינה קבועה בה אני סוקר מאמרים חשובים בתחום ה-ML/DL, וכותב גרסה פשוטה וברורה יותר שלהם בעברית. במידה ותרצו לקרוא את המאמרים הנוספים שסיכמתי, אתם מוזמנים לבדוק את העמוד שמרכז אותם תחת השם deepnightlearners.

לילה טוב חברים, היום אנחנו שוב בפינתנו deepnightlearners עם סקירה של מאמר בתחום הלמידה העמוקה. היום בחרתי לסקירה את המאמר שנקרא:

CoMatch: Semi-supervised Learning with Contrastive Graph Regularization

פינת הסוקר:  

            המלצת קריאה ממייק: מאוד מומלץ.

            בהירות כתיבה: בינונית פלוס

           רמת היכרות עם כלים מתמטיים וטכניקות של ML/DL הנדרשים להבנת מאמר: הבנת של עקרונות הלמידה הניגודית (contrastive learning) וידע בסיסי בגרפים

          יישומים פרקטיים אפשריים: הפקה של ייצוגים חזקים של דאטה עבור משימות של self-supervised/semi-cosupervised learning.

פרטי מאמר:

      לינק למאמר: זמין להורדה.

      לינק לקוד: זמין כאן.

      פורסם בתאריך: 21.03.21, בארקיב.

      הוצג בכנס: לא הצלחתי לאתר.

תחומי מאמר: 

• (Semi-Supervised Learning (SmSL
• (Self-Supervised Learning (SSL

כלים מתמטיים, מושגים וסימונים:

• (Self-Supervised Contrastive Learning (SSCL
• SSL/SmSL מבוסס על מינימיזציה של אנטרופיה 
• SmSL המבוסס על גרף של דמיונות
• פסאודו לייבלים (תוצאת הרצת רשת סיווג על דאטה לא מתויג)
• יישור התפלגות (distribution alignment) עבור פסאודו לייבלים

תמצית מאמר: 

המאמר משלב 4 גישות פופולריות מעולמות של SSL ו- SmSL:

 1. רגולריזציה על בסיס עקביות

שיטה זו מבוססת על הנחה שההסתברויות של לייבל עבור דוגמא נתונה לפני ואחרי אוגמנטציה, אמורות להיות קרובות. למשל בדומיין של התמונות ההגיון מאחורי גישה זו הינו מאוד פשוט וטבעי: מכיוון שאוגמנטציה איננה משנה את התוכן של תמונה אלא רק את סגנונה, היא לא אמורה להשפיע על התפלגות פלט המסווג. עקרון זה ניתן לתרגם למשל למינימיזציה של קרוס-אנטרופי או מרחק ריבועי בין החיזויים של הדוגמה המקורית לגרסה שלה לאחר אוגמנטציה.

  2. מינימיזציה של אנטרופיה של פלט המסווג

כאן אנחנו רוצים לבנות מסווג שמוציא "חיזויים בטוחים" לדוגמאות מהדאטהסט כלומר כאלו שלייבל אחד מקבל הסתברות גבוה משמעותית מכל האחרים. זה כמובן שקול למינימיזציה של אנטרופיה של פלט המסווג. ניתן להשיג את זה בין השאר ע"י מינימיזציה של אנטרופיה של פלט הרשת על דוגמאות לא מתויגות (בצורה מפורשת) או ע"י בנייה של פסאודו לייבלים בעלי אנטרופיה נמוכה על דוגמאות לא מתויגות ואימון של המסווג על דוגמאות אלה. 

3. (Self-Supervised Contrastive Learning (SSCL

הנחת היסוד בגישה זו אומרת כי ייצוג חזק של דאטה (במרחב במימד נמוך) מסוגל להפריד בין זוגות של הדוגמאות דומות לבין זוגות של דוגמאות רנדומליות (לא דומות). אחת הצורות הפופולריות של פונקצית מטרה במאמרי SSCL נקראת InfoNCE. ניתן להראות כי ככל שלוס InfoNCE קטן יותר, מידע הדדי בין דוגמא במרחב המקורי לבין ייצוגה במרחב ממימד נמוך עולה. זה כמובן מצביע על אובדן של פחות אינפורמציה בין הדאטה המקורי לבין ייצוגה כלומר הייצוג נהיה פחות לוסי ומייצג את הדאטה בצורה מדויקת יותר. חשוב לציין שהאימון מתבצע במרחב הייצוג ולא במרחב המקורי, כלומר הלוס מחושב על ייצוגים במרחב ממימד נמוך. לוס InfoNCE לוקח זוג של דוגמאות קרובות (למשל שתי אוגמנטציות של אותה דוגמא) ומספר דוגמאות רנדומליות ומנסה למקסם את היחס בין אקספוננט של דמיון של הזוג הקרוב לסכום הדמיונות בינו לבין דוגמאות רנדומליות. 

4. SmSL המבוססים על גרף של דמיונות

כאן בונים גרף של דמיונות של דוגמאות מהדאטהסט כאשר קודקודים של דוגמאות קרובות (תחת איזושהי מטריקה – במרחב המקורי או במרחב של לייבלים) מחוברים  בקשת במשקל גבוה, כאשר הקודקודים של דוגמאות רחוקות מחוברים בקשתות בעלות משקל נמוך או לא מחוברות כלל. לאחר מכן מאמנים ייצוגים של דאטה במרחב ממימד נמוך תוך כדי התחשבות ב״טופולוגיה של הגרף״. במילים אחרות דוגמאות קרובות אחת לשנייה (מבחינת הגרף) יאומנו לקבל ייצוגים קרובים.

הסבר של רעיונות בסיסיים: 

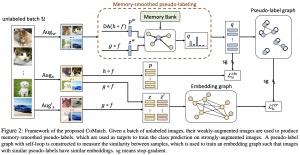
המאמר מציע שיטה, הנקראת CoMatch, שלמעשה בנויה על שילוב של 4 גישות אלו. CoMatch מנצלת את הייצוג של דוגמאות במרחב לטנטי (מימד נמוך) Z ובמרחב הלייבלים Q ומבצעת אימון בהתבסס על שני גרפים של דמיונות הנבנים בהתבסס על קשרים בין דוגמאות במרחבים אלו. נציין כי Q הינו מרחב הפלטים של רשת הסיווג כלומר הוא מכיל וקטורי הסתברויות של הלייבלים. 

אז איך זה בעצם נעשה? קודם כל בואו נבין את המבנה של פונקציה הלוס של CoMatch.

פונקצית לוס: 

נתחיל מזה שנזכר CoMatch הינה שיטה של SmSL כלומר יש לנו דאטהסט עם דוגמאות מתויגות הנקרא X, והדאטהסט של דוגמאות לא מתויגות U. נסמן את הגרף שנבנה מעל המרחב הלטנטי Z ב-G_emb ,והגרף על מרחב לייבלים Q יסומן ב-G_lab. עכשיו נוכל לעבור לתיאור הרעיונות העיקריים של המאמר:

המאמר מציע לאמן 3 רשתות: 

• רשת מקודדת f הבונה ייצוג מקדים של דאטה, המשמש גם כשלב מקדים לבניית של ייצוג הדאטה z וגם לרשת המסווגת.
• רשת, הבונה ייצוג של דאטה במרחב הלטנטי Z, שמופעלת אחרי f, המסומנת ב-g (פולטת ייצוגים מנורמלים).
• רשת סיווג h שמטרתה להוציא וקטור הסתברויות של לייבלים (גם מופעלת אחרי f) עבור פיסץ.

כעת נתאר פונקציית לוס, המוצעת במאמר. היא מורכבת מ-3 חלקים:

1. L_x: קרוס-אנטרופי לוס רגיל על דוגמאות מתויגות. כאן הלוס מחושב על דוגמאות מתויגות שעברו אוגמנטציה חלשה. הלוס מחושב בין החיזוי של דוגמא לאחר אוגמנטציה לבין הלייבל של הדוגמא המקורית.
2. L_ucls: קרוס אנטרופי לוס בין פסאודו לייבלים של דוגמא לא מתויגת לבין החיזוי עבור אותה דוגמא לאחר אוגמנטציה חזקה. נציין כי רק פסאודו לייבלים בעלי הסתברות מעל סף מסוים נלקחים בחשבון בחישוב הלוס במטרה ״לא לקנוס״ את המודל על הדוגמאות שלא הצליח לבנות להם פסאודו לייבל "אמין", כלומר בעל אנטרופיה נמוכה (FixMatch). על איך בונים את הפסאודו לייבלים האלו נדון בפרק הבא.
3. L_uctr: הלוס הניגודי (בסגנון InfoNCE) הבנוי על גרפי דמיונות על מרחבי Z ו- Q. נסביר את המבנה של לוס זה בהמשך.

כעת בואו נתעמק באיך בונים את הפסאודו לייבלים q_b הנחוצים לחישוב של L_ucls.

יצירה של פסאודו לייבליים:

קודם כל פסאודו לייבל עבור דוגמא מתויגת מוגדר בתור לייבל האמיתי (ground-truth) של הדוגמא. על דוגמא לא מתויגת מפעילים אוגמנטציה חלשה ומחשבים את ההתפלגות החזויה של הלייבלים. לאחר מכן מבצעים יישור התפלגות (DA) שמיועד למנוע מהתפלגות הלייבלים לקרוס לתת-קבוצה של הלייבלים. בשביל כך מחשבים ממוצע נע p_av (על פני האיטרציות של אימון) על כל החיזויים של הדוגמאות הלא מתויגות. למעשה p_av המהווה שערוך של שכיחות הלייבלים בדאטהסט. לאחר מכן מחלקים את וקטור ההסתברויות החזויות p_w של כל דוגמא ב-p_av. נציין שלהדביל מ-ReMixMatch, וקטור שכיחויות הלייבלים הנגזר מהדוגמאות המתויגות לא נלקח בחשבון כאן. 

כעת מחשבים גם את הייצוגים הלטנטיים z_w של הדוגמאות ע״י העברתם דרך הרשת המקודדת f ורשת הייצוג g. שומרים z_w יחד עם וקטורי התפלגות החזויים p_w במאגר של דוגמאות B. עתה נסביר איך מאמנים רשת הסיווג h, המשערכת פסאודו לייבל q_b (התפלגות מעל מרחב הלייבלים) של דוגמה לא מתויגת. כדי לאמן את h, המאמר מנסח בעיית אופטימיזציה עם פונקצית מטרה המורכבת מסכום קמור (עם מקדמים המסתכמים ל-1) של שני מחוברים. בפועל לכל באטץ' יש לנו סכום קמור של:

• סכום הריבועים של המרחקים של פלט הרשת המסווגת h (התפלגות מעל לייבלים) עבור דוגמא u_w לבין קטורי התפלגות החזויים p_wk של הדוגמאות מ-B, כאשר כל מרחק כזה ממושקל בדמיון המנורמל a_k בין הייצוג z_w של u_w לבין הייצוג הלטנטי של u_wk, המסומן כ- z_wk. המטרה של איבר זה היא לקרב את התפלגויות של פסאודו לייבלים עבור דוגמאות קרובות במרחב הייצוג. כאן דמיון בין הייצוגים מוגדר כאקספוננט של מכפלה פנימית בין הייצוגים (המנורמל בסכום של של כל הדמיוניות עבור הדוגמאות מ-B).
• מרחק ריבועי בין חיזוי עבור דוגמה p_w לבין q_b (כדי לא לשנות את התפלגות פסאודו לייבלים יותר מדי)

לבעיית אופטימיזציה זו יש פתרון מדויק וזה למעשה סכום קמור של p_w ו- p_wk-ים כאשר המקדם לפני p_wk הוא הדמיון a_k.

החלק האחרון בפאזל שטרם התייחסנו אליו הינו הלוס L_uctr, המבוסס על גרפי דמיון מעל מרחבי ייצוגים Z והלייבלים Q.

מבנה של L_uctr: לכל באטץ' בונים גרף G_lab מעל מרחב Q, כאשר משקל הקשת בין דוגמאות (קודקודים) מוגדר ע״י הדמיון (מכפלה פנימית) בין הפסאדו לייבלים של הדוגמאות (משקל של קשת עצמית מוגדרת להיות 1). אם ערכו של דמיון הוא קטן מסף מינימלי, הקודקודים של דוגמאות אלו לא מחוברים. לאחר מכן בונים גרף G_emb מעל מרחב הייצוגים. משקל קשת עצמית של קודקוד המתאים לדוגמא u ב-G_emb מוגדר כדמיון בין הייצוג של שתי אוגמנטציות חזקות של u (הדמיון הוא המכפלה הפנימית בין הייצוגים). הקשת בין כל זוג אחר של קודקודים מוגדרת כדמיון בין הייצוג של הדוגמא, המתאימה לקודקוד הראשון (לאחר אוגמנטציה חזקה) לבין הייצוג של הדוגמא מהקודקוד השני. לאחר מכן מנרמלים את הקשתות עבור שני הגרפים. 

ועכשיו בא הקטע המגניב של המאמר (לפחות בעיניי) וזה בניית הלוס המשלב את שני הגרפים האלו. מאמנים את את ייצוגי הדוגמאות שמהם נבנה גרף G_emb, כך שהוא (הגרף!!) יהיה כמה שיותר דומה מבחינת משקלי הקשתות ל-G_lab.  לוס זה מורכב משני חלקים:

• הלוס ניגודי (contrastive) בין הקשתות העצמיות של G_lab. בדומה ללוסים ניגודיים דומים הוא דוחף את המודל לתת ייצוגים דומים לאוגמנטציות שונות של אותה דוגמא. 
• החלק השני של הלוס "דוחף" ייצוגים של לדוגמאות עם פסאודו לייבלים דומים, להיות דומים (!!) (כלומר גורמים לקשת ביניהם ב- G_lab להיות בעלת משקל גבוה). לדעתי זו אחת הנקודות הכי חשובות במאמר וגם הסיבה העיקרית לכך ש-CoMatch הצליחה להגיע לביצועים טובים.

הישגי מאמר:

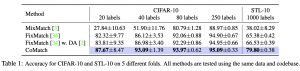
המאמר מראה שיפור בביצועים בכמה משימות SmSL קלאסיות מעל שיטות עכשוויות כמו FixMatch  ו- MixMatch.

דאטהסטים:

CIFAR100, STL10.

נ.ב.

המאמר מציע שילוב אלגנטי של 4 שיטות אימון מעולם SmSL. מאוד אהבתי את השילוב של גרפי דמיון מעל מרחבי ייצוג ומרחב הלייבלים בחישוב של הלוס הניגודי. עם זאת המאמר הראה את עליונות של CoMatch רק על שני דאטהסטים יחסית קלים. הייתי רוצה לראות את ביצועיה של גישה זאת לדאטהסטים יותר מורכבים ומקווה שזה יבוא בהמשך.  

#deepnightlearners

הפוסט נכתב על ידי מיכאל (מייק) ארליכסון, PhD, Michael Erlihson.

מיכאל עובד בחברת הסייבר Salt Security בתור Principal Data Scientist. מיכאל חוקר ופועל בתחום הלמידה העמוקה, ולצד זאת מרצה ומנגיש את החומרים המדעיים לקהל הרחב.