Layer Folding: Neural Network Depth Reduction using Activation Linearization (סקירה)

סקירה זו היא חלק מפינה קבועה של סקירת מאמרים חשובים בתחום ה-ML/DL, בהם מוצגת בעברית גרסה פשוטה וברורה של מאמרים נבחרים. במידה ותרצו לקרוא את המאמרים הנוספים שסוכמו, אתם מוזמנים לבדוק את העמוד שמרכז אותם תחת השם deepnightlearners.

לילה טוב חברים, היום אנחנו שוב בפינתנו deepnightlearners עם סקירה של מאמר בתחום הלמידה העמוקה. היום בחרתי לסקור מאמר שאני שותף בכתיבה שלו, יחד עם שותפים מ-SIRC – Samsung Israel R&D Center:

Layer Folding: Neural Network Depth Reduction using Activation Linearization

מאת: Amir Ben Dror, Niv Zehngut, Avraham Raviv, Evgeny Artyomov, Ran Vitek, Roy Jevnisek.

פינת הסוקר:

    המלצת קריאה: מומלץ מאוד לכל מי שמתעסק ברשתות נוירונים מיועדות למכשירי קצה (מובייל, IoT וכדו').

    בהירות כתיבה: גבוהה.

    רמת היכרות עם כלים מתמטיים וטכניקות של ML/DL הנדרשים להבנת מאמר: נדרשת היכרות בסיסית עם רשתות קונבלוציה. המאמר קל להבנה וכמעט לא מכיל נוסחאות מתמטיות.

    יישומים פרקטיים אפשריים: יצירת רשתות פחות עמוקות המקנות שיפור ב-inference time וצריכת סוללה כמעט ללא פגיעה בדיוק הרשתות.

פרטי מאמר:

    לינק למאמר: זמין כאן

    לינק לקוד: זמין כאן (PyTorch)

    פורסם בתאריך: 17.06.21, בארקיב

רקע ותמצית המאמר:

הרצה של רשתות נוירונים על מכשירים דלי משאבים כמו מובייל, מצלמות חכמות וכדו', הינה משימה מאתגרת. כיוון שמשאבי המכשיר מוגבלים, החישובים איטיים יחסית ובנוסף צורכים הרבה סוללה. אתגרים אלו הובילו לתכנון רשתות יעילות, דוגמת MobileNet ו-EfficientNet, במקביל לפיתוח שיטות להקטנת רשתות (pruning, quantization ועוד). אלמנט מרכזי המהווה צוואר בקבוק במהירות החישוב (inference time) הינו עומק הרשת. פעולות על שכבה מסוימת יכולות להתקיים באופן מקבילי, אך לא ניתן לבצע חישובים על שתי שכבות שונות במקביל, כיוון שיש קודם לסיים להעביר את כל המידע לשכבה העמוקה פחות ורק אחר כך לבצע את החישובים על השכבה עמוקה יותר מתוך השתיים. לכן הגיוני לשאוף לקבל רשת עם מעט שכבות. עם זאת, העומק מעניק לרשת את היכולת לבצע למידה על משימות מורכבות, ולכן שימוש במעט שכבות יכול לפגוע בביצועי הרשת. כדי להתמודד עם הטרייד-אוף הזה, התפתחו שיטות שמאמנות רשת עמוקה עם הרבה שכבות, ולאחר מכן מחפשות דרכים להסיר שכבות עם פגיעה מינימלית בביצועים.

במאמר הנסקר מוצעת דרך פשוטה ואלגנטית למשימה זו, כלומר דרך קלה להסרת שכבות עם פגיעה מינימלית בביצועים. השיטה מראה כיצד מושג שיפור ב-inference time, כלומר בזמן שלוקח לרשת המאומנת לבצע משימה כלשהיא, כגון סיווג, זיהוי אובייקטים וכדו'. מלבד התוצאה המספרית בנוגע ל-inference time, עולה במאמר נקודה יפה נוספת – השיטה המוצעת מאפשרת למצוא את מספר השכבות המינימלי הדרוש בשביל להגיע לאחוז דיוק מסוים למשימה נתונה, ואם משתמשים בפחות שכבות – הדיוק צונח. מספר זה, כך נטען, יכול לאפיין את הבעיה מבחינת רמת ה"אי לינאריות" שלה, קרי, מה מספר האקטיבציות הלא לינאריות המינימלי הדרוש עבור קבלת תוצאות טובות לבעיה ספציפית (אמנם במאמר מדגימים נקודה זו על משימות סיווג, אך אפשר להשתמש בשיטה גם עבור משימות אחרות).

תקציר המאמר:

בכל רשת ישנן אקטיבציות לא לינאריות. נגדיר parametric activation באופן הבא:

Parametric activation = α·Identity + (1-α)·activation

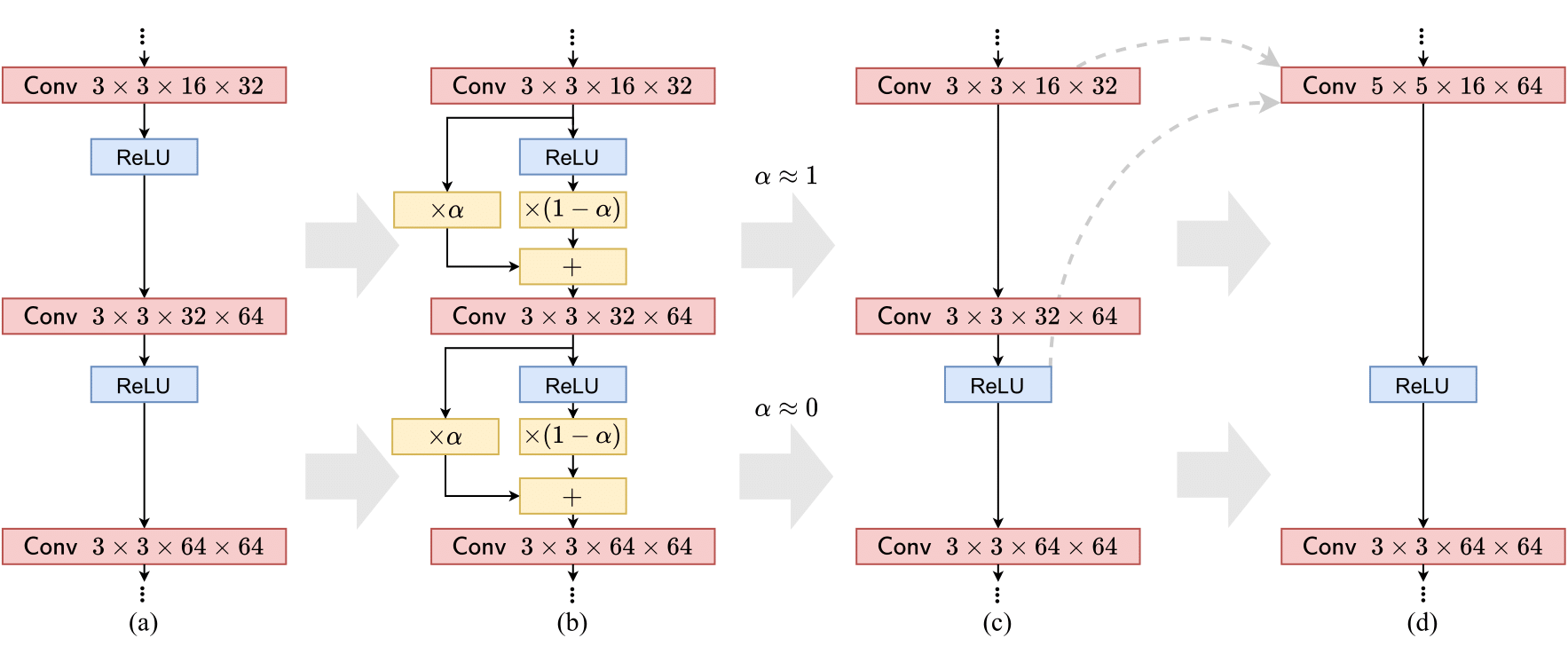
נשים לב שאם α=0, מתקבלת האקטיבציה כמו שהיא, ואילו אם α=1 אז מתקבלת פונקציית הזהות. כעת ניקח רשת מאומנת, ונחליף את האקטיבציות באקטיבציות עם פרמטר, כאשר נאתחל את כל הפרמטרים ב-0, כלומר α=0. למעשה בהחלפה זו לא התבצע שום שינוי, והרשת נשארת כמו שהיא. כעת מה שנרצה לעשות זה "לדחוף" את כל ה-α מ-0 ל-1 ובכך להפוך את האקטיבציות מפונקציות לא לינאריות לפונקציות לינאריות (ובפרט – לפונקציית הזהות). עבור אקטיבציה בה הפרמטר α מגיע ל-1, הפעולה של האקטיבציה הינה לינארית לחלוטין, ולכן ניתן לאחר האימון לחבר את השכבה שלפני האקטיבציה עם השכבה שאחריה (כיוון שכל הפעולות לינאריות), ובכך ליצור רשת עם פחות שכבות.

לפני שנסביר איך ניתן לעשות את זה, נדגים על האקטיבציה ReLU. למעשה, כבר קיימת גרסה פרמטרית ל-ReLU, והיא מוכרת בשם Parametric ReLU או בקיצור PReLU. בעוד ReLU=max(0,x), הגרסה הפרמטרית הינה: PReLU=max(αx,x). עבור α=0, יש זהות בין האקטיבציות, כלומר PReLU=RELU, ואילו עבור α=1 מתקיים PReLU=x, כלומר פונקציית הזהות, שלמעשה הינה לינארית לחלוטין. כעת אם יש רשת עם ReLUs, ניתן להחליף אותם ב-PReLUs עם פרמטר התחלתי 0, ולנסות להביא אותו ל-1, ובכך להוריד חלק מהאקטיבציות הלא לינאריות.

אוקי, אז איך עושים את הקסם הזה ומביאים את ה-α מ-0 ל-1? בעזרת איבר נוסף בפונקציית המחיר (Loss function). נניח ופונקציית המחיר של המשימה המקורית הינה ℒ_t, אז ניתן להוסיף עבור כל α איבר auxiliary loss מהצורה |(1-α²)|λ. נשים לב שאם α קרובה ל-0 אז הביטוי |1-α²| קרוב ל-1, ואם α קרובה ל-1 אז הביטוי |1-α²| קרוב ל-0, ולכן איבר זה ירצה לגרום ל-α לטפס מ-0 ל-1. הפרמטר λ הינו פרמטר שבא לאזן בין המחיר של המשימה המקורית לבין המחיר שמשלמים על α שקרובות ל-0. (הערה: היה ניתן להשתמש גם בביטויים אחרים בפונקציית המחיר לצורך משימה זו, כפי שמצוין במאמר, ונבחר דווקא איבר זה כיוון שהוא יחסית פשוט). כמובן שצריך להוסיף את איבר ה-auxiliary loss עבור כל α, וכן הפרמטר λ יכול להיות שונה עבור כל α, אך במאמר נקטו בדרך הפשוטה והכללית, ובסך הכל פונקציית המחיר הינה:

ℒ=ℒ_t+∑_i|1-α²_i|·λ

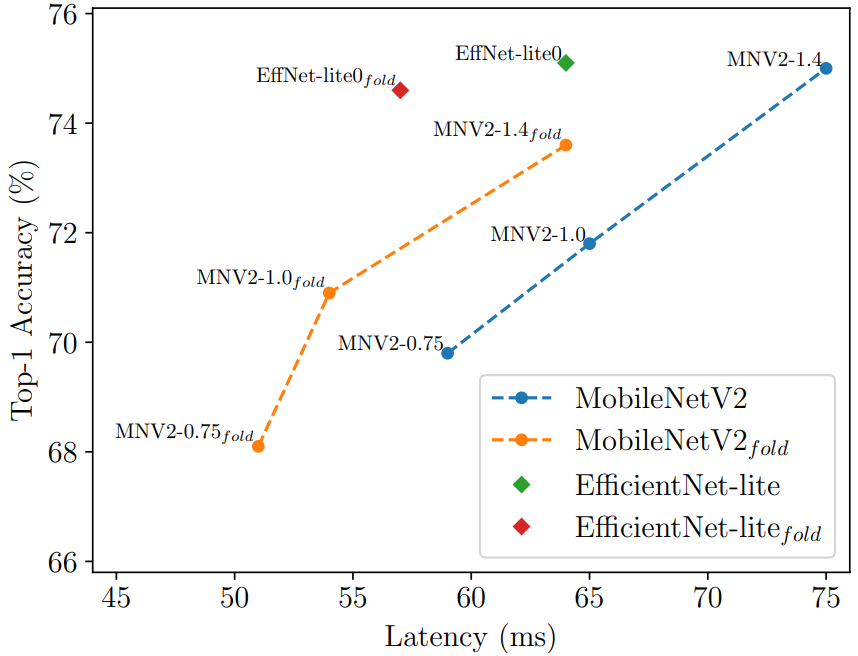
לאחר החלפת האקטיבציות לאקטיבציות עם פרמטרים והוספת האיבר לפונקציית המחיר, כל שנותר לעשות זה לקחת את הרשת המאומנת, לבצע עליה עוד אימון, ולקבל ביטול של חלק מהאקטיבציות, תוך כדי כך שהאיבר הראשון בפונקציית המחיר דואג לעדכן את המשקלים כך שהדיוק עבור המשימה המקורית יפגע כמה שפחות. במאמר מראים תוצאות על ImageNet עבור רשתות שונות וכיצד באמצעות שיטה זו יש שיפור בזמן החישוב תוך פגיעה מינימלית בדיוק.

הערה חשובה: לאחר שמצליחים להביא α ל-1, נותר לבצע "קיפול" של הרשת, כלומר איחוד של שתי שכבות עם פעולה לינארית ביניהן. אם מדובר בשכבות קונבולוציה, כדי לשמור על ה-activation map, יש להגדיל את הקרנל בשכבה המאוחדת ביחס לשכבות המקוריות. למרות שהגדלת הקרנל מגדילה בדרך כלל את מספר ההכפלות הדרושות, בסך הכל עדיין יש שיפור במהירות החישוב כיוון שמספר השכבות ירד ב-1 ואילו חישובים על הקרנל יכולים להתבצע במקביל. במובן הזה השיטה נבדלת משיטות pruning, כיוון שהמטרה שלהן היא להקטין את הרשת, ואילו במאמר זה הרשת לא בהכרח קטנה אלא להיפך – לרוב אך בזכות רידוד הרשת מתקבל שיפור בזמן החישוב.

כאן למעשה השיטה מילאה את תפקידה המקורי – למצוא דרך פשוטה ונוחה להפחית את עומק הרשת תוך שמירה על הביצועים כמה שניתן. אך במאמר מעלים נקודה נוספת, יפה לא פחות מהראשונה. נתבונן שוב באיבר שנוסף לפונקציית המחיר. אם הפרמטר λ יהיה מאוד גדול, כל מה שהרשת תנסה זה רק לבטל את האקטיבציות, בלי להתחשב במשימה המקורית. לאחר אימון עם כזה פרמטר תתקבל רשת לינארית עם ביצועים גרועים. אם לעומת זאת הפרמטר λ קרוב ל-0, הרשת תתמקד במשימתה המקורית ולא ממש תנסה לבצע את נרמול האקטיבציות. וכאן נשאלת השאלה – מה קורה עבור ערכי λ שונים, שאינם גדולים מאוד אך גם אינם קרובים ל-0?

אז פה נכנסת הנקודה השנייה של המאמר. נניח ולוקחים ארכיטקטורה מסוימת, למשל ResNet20, ומבצעים עליה אימון עם אקטיבציות עם פרמטרים ופונקציית מחיר כפי שתואר לעיל. עבור ערכי λ שונים יתקבלו עומקים שונים – ככל ש-λ יגדל, כך יתקפלו יותר שכבות. במאמר מראים שיש נקודה מסוימת שמעבר אליה אם מורידים עוד שכבות אז הדיוק צונח. כלומר, יש מספר מסוים של אקטיבציות לא לינאריות שחייבים לשמור עליו בכדי להישאר עם ביצועים טובים. במאמר מראים שעבור משימה מסוימת, אם לוקחים רשתות שונות – לכולן יש את אותו מספר שכבות מינימלי שיש לשמור עליו. בין אם מתחילים מ-56 שכבות ובין אם מתחילים מ-20 שכבות, כל הרשתות מתכנסות לאותו מספר של אקטיבציות לא לינאריות, שמתחתיו הדיוק צונח.

נקודה זו מכונה במאמר "Effective Degree of Non-Linearity", והיא בעצם מאפיין של הבעיה עצמה ופחות של הארכיטקטורה. יוצא בעצם שהשיטה המוצעת במאמר, מלבד היכולת שלה לשפר את זמני החישוב, משמשת גם ככלי פשוט למדידת רמת אי-לינאריות של בעיה מסוימת. במאמר לא מסתפקים בזה, ומראים גם טבלאות של איזה אקטיבציות התקפלו ואיזה נשארו. טבלאות אלה יכולות ללמד מה השכבות היותר משמעותיות ועל אלה ניתן לוותר כמעט בלי פגיעה בביצועים בכל ארכיטקטורה של רשת. כך למשל ניתן לראות שב-VGG השכבות הראשונות מהותיות ואילו את השכבות שבסוף ניתן להסיר, ואילו ב-ResNet זה לא כך אלא השכבות שלא מוסרות מפוזרות באופן די אחיד על פני הרשת.

עוד מראים במאמר שאם מראש היו לוקחים את מבנה הרשת שהתקבל לאחר הקיפול וחיבור השכבות ומאמנים כזו ארכיטקטורה from scratch, לא מצליחים להגיע לאותו דיוק של רשת שמראש הייתה עמוקה וביצעו עליה קיפולי שכבות ו-fine tuning. הסיבה נעוצה בכך שהרשת העמוקה כבר למדה intermediate representation של הבעיה, וייצוג זה נשמר בתהליך קיפול השכבות מה שמאפשר לביצועים להישאר גבוהים. מה שאין כן ברשת פחות עמוקה שצריכה ללמוד מאפס – כיוון שאין לה מידע כלשהו, היא לא מצליחה לספק את אותם ביצועים. בכך מדגישים במאמר את החשיבות של השיטה – היא לא רק מספקת רשת עם פחות שכבות, אלא היא גם דואגת שהביצועים יישארו טובים, ובוודאי גבוהים יותר מאלו של רשת שמראש נבנתה עם פחות שכבות.

סיכום והישגי המאמר:

המאמר מציג שיטה מאוד פשוטה לנרמול אקטיבציות (או אם תרצו: activation pruning). פעולה זו מביאה לשיפור ב-inference time, ובנוסף מאפשר להבין דברים על בעיות וארכיטקטורות, כמו למשל מה רמת האי לינאריות של בעיה, ומהן השכבות היותר חשובות בארכיטקטורה מסוימת. מלבד זאת שהשיטה אלגנטית, היא גם מאוד קלה למימוש, ויש קוד פתוח שמצורף למאמר. יש לציין שהשיטה אינה מתאימה לכל ארכיטקטורה, כמו למשל ארכיטקטורות בהן הקיפול מגדיל את הקרנלים של הקונבולוציות לממדים גדולים מאוד, רשתות שמשתמשות ב-squeeze-and-excite ועוד.

נ.ב.

מאמר כתוב היטב עם רעיון פשוט להורדת כמות השכבות ברשת תוך מינימום פגיעה בביצועים, ובנוסף אפיון של רמת אי לינאריות של משימות. המאמר מספק תמונה מקיפה מאוד של הנושא וכתוב בצורה מאוד קריאה ונוחה, ובנוסף מוצג קוד פשוט למימוש השיטה.

#deepnightlearners

הפוסט נכתב על ידי אברהם רביב.