Unsupervised Discovery of Interpretable Directions in the GAN Latent Space (סקירה)

סקירה זו היא חלק מפינה קבועה בה אני סוקר מאמרים חשובים בתחום ה-ML/DL, וכותב גרסה פשוטה וברורה יותר שלהם בעברית. במידה ותרצו לקרוא את המאמרים הנוספים שסיכמתי, אתם מוזמנים לבדוק את העמוד שמרכז אותם תחת השם deepnightlearners.

לילה טוב חברים, היום אנחנו שוב בפינתנו deepnightlearners עם סקירה של מאמר בתחום הלמידה העמוקה. היום בחרתי לסקירה את המאמר שנקרא:

Unsupervised Discovery of Interpretable Directions in the GAN Latent Space

פינת הסוקר:        

       המלצת קריאה ממייק: מומלץ לעוסקים ב-GANs לשאר רק אם יש זמן פנוי.

       בהירות כתיבה: גבוהה.

       רמת היכרות עם כלים מתמטיים וטכניקות של ML/DL הנדרשים להבנת מאמר: היכרות עם עקרונות של GANs מספיקה.

      יישומים פרקטיים אפשריים: מציאת כיוונים במרחב הלטנטי הגורמים לשינוי של מאפיין ויזואלי בודד של התמונה המגונרטת.

פרטי מאמר:

      לינק למאמר: זמין כאן

      לינק לקוד: זמין כאן

      פורסם בתאריך: 24.06.2020, בארקיב

      הוצג בכנס: ICML 2020

תחום מאמר:

• GANs 
• חקר של המרחב הלטנטי של GANs

כלים מתמטיים, מושגים וסימונים:

• וקטור (כיוון) בר פירוש (interpretable direction).

תמצית מאמר: 

המאמר הנסקר מציע שיטה למציאה של וקטורי (כיוונים) ״ברי פירוש״ (interpretable directions) במרחב לטנטי של GAN מאומן. וקטור בר פירוש v_int מוגדר ככזה שהוספתו לכל וקטור v מהמרחב הלטנטי של GAN מאומן, שהשינוי בין התמונות המגונרטות באמצעות וקטורים אלה (v ו- v + v_int), יהיה במאפיין ויזואלי אחד בלבד של כגון צבע גוון עור, צורת גבות, רקע וכדומה. השיטה המוצעת לא תלויה בארכיטקטורה של GAN ולא דורשת שום supervision (!!).

רעיון בסיסי:

הנחת יסוד של המאמר אומרת שכיוונים ברי פירוש שונים גורמים לטרנספורמציות בעלות שוני רב של התמונה, כלומר כאלו שניתן להבחין בין טרנבפטרמציה אחת לאחרת בקלות. לכן בתהליך הלמידה המחברים מנסים לאתר (ללמוד) כיוונים במרחב הלטנטי הגורמים לטרנספורמציות שונות מאוד בתמונות הנוצרות.

תקציר מאמר: 

כפי שצוין במאמר מחקרים המתמקדים בחיפוש כיוונים ברי פירוש במרחב לטנטי של GAN מערבים supervision כלשהו בתהליך החיפוש. מה שנהוג לעשות הוא לבצע טרנספורמציות ברות פירוש לתמונות (סיבוב, הקטנה, הוספת משקפיים וכדומה) ולראות איזה כיוונים במרחב הלטנטי גורמים לשינויים האלו. קו נוסף של מחקר בנושא זה מתמקד בבנייה של גאנים בעלי פיצ'רים לא מעורבבים (disentangled) שמהם ניתן להפיק כיוונים ברי פירוש יחסית בקלות. המאמר מציין אימון גאן עם פיצ'רים לא מעורבב זו משימה קשה (שזה נכון) וגם טוען שהתוצאות של מודלים כאלו לא מרשימות במיוחד יחסית ל-SOTA ונותן דוגמאות של InfoGAN, OoGAN, ID-GAN אבל משום מה לא מתייחס למשל ל-StyleGAN2 שיצא כמה חודשים לפני פרסום המאמר הנסקר. דרך נוספת לנתח כיווני ברי פירוש בגאנים היא לחקור ו"ע של מטריצת יקוביען של הגנרטור.

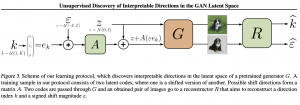
המאמר מציע שיטה ״ישירה״ יותר לפתרון של בעיית חיפוש כיוונים ברי פירוש במרחב לטנטי של GAN. השיטה המוצעת לוקחת רשת גנרטור מאומנת ומנסה למצוא K (שווה בדרך כלל זה מימד של הקלט של הגנרטור) וקטורים ברי פירוש במרחב הלטנטי. החיפוש נעשה בדרך מאוד פשוטה האינטואיטיבית. מאמנים רשת כאשר וקטורים ברי פירוש הם חלק מהמשקלים שלה. למעשה המחברים לא עושים שום טרנספורמציה מפורשת לתמונה כמו שנהוג לעשות במאמרים הקודמים אלא רק "משחקים" עם המרחב הלטנטי. בגדול המאמר מציע להגריל וקטור z מהמרחב הלטנטי של הגאן המאומן ולחבר לוקטור הזה וקטורי בר פירוש מאומן v. לאחר מכן מגנרטים שתי תמונות באמצעות הזנתם z ו- z + v לגנרטור מאומן. בשלב האחרון מזינים את התמונות הללו לרשת שמנסה לשערך מהו הכיוון של וקטור v המוסף ל-z.

כעת ניתן תיאור יותר מפורט של השיטה המוצעת: 

אימון הרשת למציאת וקטורי ברי פירוש:

1. מגרילים את מספר הכיוון k (בין 1 ל-K) ויוצרים מזה וקטור h 1hot. 
2. מגרילים גודל (אורך) a של וקטור זה (מהתפלגות יוניפורמית סימטרית סביב 0).
3. מכפילים הוקטור v = ah במטריצה A עם משקלים מאומנים (A למעשה מכילה וקטורי בר פירוש שאנחנו מנסים לשערך/ללמוד (בדומה לבנייה של וקטור ייצוג למילה ממילון נתון ב-word2vec).
4. מגרילים וקטור z מהמרחב הלטנטי שך גאן מהתפלגות גאוסית סטנדרטית.
5. מגנרטים שתי תמונות, הראשונה מ-z והשנייה  מ-z+v באמצעות הזנתם לגנרוטור המאומן.
6. מעבירים שתי תמונות אלו דרך רשת עם משקלים מאומנים R כאשר מטרתה לשערך את מספר הכיוון k ואת הגודל שלו a (ז״א הפלט של R הוא וקטור הסתברויות K-מימדי ומספר ממשי).

חשוב להבין שהמשקלים של R והמשקלים של מטריצת הכיוונים A מאומנים ביחד. עקב כך תוך כדי תהליך האימון העמודות של מטריצה A מנסות ״לפשט״ את בעיית הסיווג  שהרשת R מנסה לפתור,״באמצעות התכנסות" לכיוונים קלים יותר להבחנה.

 פונקציית לוס: פונקציית לוס מורכבת משני מחוברים: הראשון הוא איבר קרוס-אנטרופי סנדרטי על השערוך של מספר הכיוון k והשני הוא הלוס הריבועי על השערוך של a. האיבר השני מהווה רגולריזציה המיועדת לכפות על אורך של וקטור הכיוון להשפיע באופן רציף על התמונה המגונרטת במטרה למנוע מיפוי של כל הכיוונים לקבוצה קטנה של תמונות.

הערה לגבי מטריצת הכיוונים: המחברים ניסו לבחור מטריצת כיוונים משתי צורות – בעלת עמודות עם אורך 1 ומטריצה אורתונורמלית (עמודות אורתוגונליות בעלות אורך 1). עבור דאטהסטים שונים צורות שונות של מטריצת כיוונים הציגו ביצועים יותר טובים מהשתיים שנבדקו, אך לא מצאתי התייחסות או דיון בסוגייה זו במאמר.

הישגי מאמר:

בסופו של דבר חלק הכיוונים (לא מצאתי מה האחוז) שהתקבלו כתוצאה מהתהליך הזה אכן נמצאו כגורמים לשינויים במאפיין אחד של התמונה. שינויים אלו ניתנים להבחנה עי״ עין אנושית (כגון צבע שער, סיבוב של תמונה, גוון עור, אודם וכדומה). דבר מעניין שהמחברים הצליחו לגלות הוא שאחד הכיוונים שהם מצאו הוא אחראי על הרקע של התמונה שאיפשר להם לטעון שהם מצאו דרך לעשות אוגמנטציה טובה לדאטהסטים למגוון משימות. מעניין שהמאפיינים הויזואליים שמתאימים לכיוונים ברי פירוש שנמצאו, משתנים (!!) בין מודלי GAN שונים ובין דאטהסטים שונים. אציין כי בנוסף להבחנה האנושית, מטריקה נוספת לשערוך ביצועים שהמאמר השתמש בה היא דיוק שחזור (RCA) הכיוון k ברשת R. כמובן ש-RCA גבוה לא מעיד על כך שמצאנו כיוון בר פירוש חזק כי קיימים שילובים של כמה מאפיינים בתמונה קלים להבחנה. 

דאטהסטים: MNIST, AnimeFaces,  Imagenet and CelebA-HQ

סוגי GAN שנבדקו: Spectral Norm GAN, ProGAN, BigGAN

נ.ב. מאמר עם רעיון נחמד, אך קצת לא מבושל. מעבר לאינטואיציה הבסיסית לא מצאתי הסברים למה הרעיון שלהם עבד. גם הייתי רוצה לראות דיון מעמיק יותר בתלות בין הכיווני ברי פירוש שנמצאו לבין הדאטהסט שעליו אומן GAN ובארכיטקטורה של GAN. בקיצור נראה שהכיוון הזה רק בתחילת דרכו ומקווה לראות את ההמשך. 

#deepnightlearners

הפוסט נכתב על ידי מיכאל (מייק) ארליכסון, PhD, Michael Erlihson.

מיכאל עובד בחברת הסייבר Salt Security בתור Principal Data Scientist. מיכאל חוקר ופועל בתחום הלמידה העמוקה, ולצד זאת מרצה ומנגיש את החומרים המדעיים לקהל הרחב.