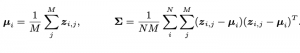Improving Self-supervised Learning with Automated Unsupervised Outlier Arbitration: סקירה

סקירה זו היא חלק מפינה קבועה בה שותפיי ואנוכי סוקרים מאמרים חשובים בתחום ה-ML/DL, וכותב גרסה פשוטה וברורה יותר שלהם בעברית. במידה ותרצו לקרוא את המאמרים הנוספים שסיכמנו, אתם מוזמנים לבדוק את העמוד שמרכז אותם תחת השם deepnightlearners.

לילה טוב חברים, היום אנחנו שוב בפינתנו deepnightlearners עם סקירה של מאמר בתחום הלמידה העמוקה. היום בחרנו לסקירה את המאמר שנקרא: 

Improving Self-supervised Learning with Automated Unsupervised Outlier Arbitration

פינת הסוקר:  

      המלצת קריאה ממייק ואברהם: שווה קריאה לחובבי למידה ייצוגית (unsupervised learning).

      בהירות כתיבה: בינונית

     ידע מוקדם: 

• הבנה בעקרונות הבסיסיים של למידה יצוגית.
• הבנה בשיטות אימון ניגודיות (contrastive).
• importance sampling.

   יישומים פרקטיים אפשריים: שיפור באיכות ייצוג של דאטה המופק באמצעות מגוון שיטות של למידה ייצוגית

פרטי מאמר:

      מאמר: זמין להורדה.

      קוד: כאן

      פורסם בתאריך: 15.12.21, בארקיב.

      הוצג בכנס: NeurIPS 2021 Poster

תחומי מאמר:

• self-supervised learning

כלים מתמטיים, מושגים וסימונים:

• Importance sampling
• Radon-Nykodim derivative

מבוא:

אחת הדרכים המקובלות ביותר להגדיל את מאגר הדאטה לאימון של מודל היא באמצעות אוגמנטציות – לוקחים דוגמאות מהמאגר שיש לנו ומשנים אותן במגוון צורות. למשל, נניח ויש לנו תמונה של חתול, אז גם סיבוב של התמונה, חיתוך שלה בזוויות שונות, שינוי הגודל ועוד כמה טרנספורמציות (אוגמנטציות) נוספות, אינן אמורות לשנות את העובדה שבתמונה יש חתול. על ידי פעולות פשוטות אלו ניתן לייצר מתמונה אחת עוד תמונות רבות השייכות לאותה קטגוריה. העובדה שאוגמנטציות מסוימות של הדוגמה המקורית שייכות לאותה הקטגוריה כמו הדוגמה המקורית הינה בעלת ערך מוסף, כיוון שלא רק הגדלנו את הדאטהסט אלא הוספנו דוגמאות מתויגות. גם כאשר אין לנו כלל דאטה מתויג ואנו רוצים להפיק ייצוג חזק של דאטה שעשוי לשמש למשימות downstream, אוגמנטציות יכולות להועיל מאוד לה כדי ״לרמוז״ למודל לגבי פיצ'רים סמנטיים חשובים של הדאטה.

ההנחה המסתתרת מאחורי השימוש באוגמנטציות הינה פשוטה והגיונית, אך כפי שנראה, היא לא תמיד מתקיימת. בעצם אנו מניחים כי הדוגמאות הן אינווריאנטיות לאוגמנטציות, כלומר טרנספורמציות מסוימות אינן משנות את המאפיינים העיקריים של הדוגמה: התמונה לאחר אוגמנטציה עדיין שייכת לאותה קטגוריה, והתוכן הסמנטי שלה נשמר. במאמר הנסקר מערערים על הנחה זו ומראים שהיא עלולה להיות בעייתית. המחברים מראים  דוגמאות שעבורן אוגמנטציות מסוימות משנות את התוכן הסמנטי של התוצאה.

המחברים דנים באימון מודלים על דאטה לא מתויג ומראים כי אוגמנטציות עלולות לפגוע ביכולת ההכללה של המודל המאומן, ומציעים פתרון אלגנטי להתמודדות עם בעיה זו.

הרעיון הבסיסי:

הסבר על הבעיה:

כאמור המאמר מנסה לטפל בבעית דוגמאות חיוביות ״שקריות״ שעלולה לעלות במהלך למידת ייצוג (representation learning) בפרט כאלה שמבוססות על שיטות ניגודיות (contrastive methods). בשיטות למידה ניגודית זוג דוגמאות חיוביות מוגדר בנוי משתי אוגמנטציות של אותה דוגמא. ההנחה המרכזית בשיטות אלו אומרת כי דוגמאות אלו הן בעלות אותו תוכן סמנטי. בדומיין הויזואלי (קרי תמונות) זוג של דוגמאות חיוביות יכול להיות שני פאצ'ים שונים (או crops) של אותה תמונה או שתי טרנספורמציות של אותה תמונה (למשל שני סיבובים שונים).

אך גישה פשטנית זו טומנת בחובה מוקש פוטנציאלי: למשל אם בתמונה יש שתי חיות, חתול וכלב, זוג של דוגמאות חיובית עלול להכיל פאץ׳ בו מוצג כלב ופאץ׳ שני בו מוצג חתול. פונקציית הלוס הניגודי תנסה לקרב את הייצוגים של שני הפאצ'ים, על אף שהתוכן הסמנטי שלהם מאוד שונה.

נזכיר כי ההנחה המרכזית מאחורי שיטת למידה ניגודית אומרת כי ייצוגים של דוגמאות ״דומות״ (= חיוביות) צריכים להיות קרובים במרחב הייצוג והייצוגים של דוגמאות לא דומות צריכים להיות רחוקים.

הערה: ניתן להשתמש בשיטה המוצעת במאמר גם עבור שיטות למידת ייצוג שלא משתמשות באופן מפורש בהנחת היסוד של הגישה הניגודית (קירוב ייצוגיים של דוגמאות חיוביות והרחקה של אלו עבור דוגמאות שליליות). בין השיטות הללו נמנות בין השאר SwaV ו- ByOL (אשר משתמש בזוגות חיוביים בלבד). בהמשך נדון בעיקר בשימוש בשיטה המוצעת עבור גישות ניגודיות קלאסיות.

המאמר הנסקר מנסה לתת מענה לבעיית הזוגות החיוביים ה-״שקריים״ באמצעות משקול אדפטיבי כאשר תרומה של כל זוג חיובי תהיה פרופורציאונלית למידת ״אמיתיות״ שלו. כלומר, עבור זוג דוגמאות חיוביות נשערך את הסבירות שהן אכן מכילים את אותו התוכן הסמנטי. ככל שהסבירות הזאת גבוהה יותר, הציון שהזוג מקבל הוא גבוה יותר והתרומה שלו לפונקציית הלוס גם היא גבוהה יותר. גישה זו דומה ל-Importance Sampling, טכניקה לדגימה מהתפלגויות מורכבות הממשקלת באמצעות דגימה והתפלגות פשוטה יותר ומשקול של דגימות אלו.

פרטים נוספים על הרעיון:

כעת נבין את העקרונות המתמטיים של הגישה המוצעת במאמר. קודם כל ניזכר במבנה של פונקציית הלוס של שיטת למידת ייצוג כלשהי. פונקציית לוס זו היא ממוצע של ערכי הלוס על פני מספר מיני-באצ'ים בנויים מזוגות חיוביים (ולפעמים מיני-באץ' כולל גם דוגמאות שליליות, הנבחרות בדרך כלל רנדומלית). ערך פונקציית לוס של מיני-באץ' הוא סכום ערכי פונקציית L עבור הזוגות המרכיבים מיני-באץ'. אבל מה היא L?

פונקציית L מקבלת ייצוגים של דוגמאות חיוביות (ולפעמים שליליות) ומודדת ״מידת התאמה של ייצוגים אלו להנחת היסוד של השיטה״.

דוגמאות של פונקציה עבור כמה שיטות למידת הייצוג:

• MoCO – פונקציה L היא יחס מרחקים בין ייצוגים של זוגות ליליים לבין אלה של הזוגות החיוביים.
• SWaV – פונקציה L היא מרחק בין קלאסטרים של דוגמאות חיוביות.
• ByOL -פונקציה L היא מרחק L2 בין ייצוגי דוגמאות חיוביות (אין דוגמאות שליליות). 

אחר מכן, מגרילים סט דוגמאות חיוביות (ולפעמים גם שליליות) ומחשבים את הערך של L על הסט הזה.

עכשיו נשאלת השאלה מאיזו התפלגות אנו דוגמים טרנספורמציות (אוגמנטציות) המניבות לנו זוגות חיוביים. קודם כל, רצוי להשתמש בזוגות של טרנספורמציות שייצרו תמונות בעלות תוכן סמנטי זהה, או לפחות דומה, בסבירות גבוהה. אולם חוק התפלגות (נסמן אותו ב-P) של זוגות טרנספורמציות כאלו אינו ידוע ובנוסף הטרנספורמציות עשויות להיות תלויות בדוגמה עצמה. כלומר, שני קרופים זהים יכולים להכיל תוכן סמנטי זהה לתמונה אחת (למשל שני חתולים) ותוכן שונה לגמרי (למשל חתול ודשא) עבור תמונה אחרת.

במטרה להתגבר על המכשול הזה ולדגום מההתפלגות הטרנספורמציות הזו, נשתמש בשיטה הנקראת (importance sampling (IS. כאמור IS מאפשרת לדגום מהתפלגות P, אשר ניסיון לדגום ממנה באופן ישיר יצריך דגימות רבות, באמצעות התפלגות אחרת Q, ממנה ניתן לדגום יותר בקלות. המשקל של דגימה x הוא היחס (P(x)/Q(x. כלומר, דגימות בעלות יחס גבוה מקבלות משקל גדול יותר ולהיפך. במקרה שלנו, ההתפלגות Q תהיה ההתפלגות שממנה אנו דוגמים אוגמנטציות לבנייה של זוגות חיוביים של דוגמאות.אבל יש לנו בעיה כאן. אנחנו לא יודעים לחשב את P(x) באופן מפורש, כלומר אין לנו דרך לדעת מהי ההסתברות שזוג אוגמנטציות יוביל לתמונות בעלות אותו תוכן סמנטי. למזלנו אנחנו כן יכולים לחשב בקירוב את היחס של P ו-Q וזה למעשה הרעיון העיקרי של המאמר. הקירוב מתבסס על כך שרוב האוגמנטציות שבדרך כלל משתמשים בהם בלמידת ייצוג כן שומרות על אותו תוכן סמנטי ויש יחסית מעט כאלו שלא מקיימות את התכונה הזו. התובנה העיקרית היא שניתן לזהות אוגמנטציות שלא מקיימות את התכונה הזאת באמצעות ניתוח של מרחק מהייצוג הממוצע zmean המתקבל מתמונה נתונה לאחר הפעלת מספר אוגמנטציות (מסומן בתור M במאמר). כלומר אם ייצוג של תמונה לאחר אוגמנטציה A רחוק מדי מ- z_mean (גם השונות נלקחת בחשבון כאן) אז ניתן להסיק כי A אינה שומרת על התוכן הסמנטי.

אם כך, המשקל w של אוגמנטציה A  מוגדר כמרחק ייצוג הדוגמה לאחר A מהייצוג הממוצע z_mean (במונחי שונות המחושבת על פני כל הדוגמאות במיני-באץ'):

כאשר הפרמטר τ  שולט ב״יחס התלות" של משקל w במרחק הנ״ל, וככל שהוא נמוך יותר המשקל יהיה יותר תלוי במרחק מהממוצע.

אופן מעט יותר פורמלי: נסמן את ההתפלגות של האוגמנטציות ה"רצויה" ב-P. התפלגות זו אינה ידועה לנו, ונדגום ממנה באמצעות היוריסטיקה מהתפלגות Q, המכילה את כל האוגמנטציות ״הרגילות״ שבדרך כלל שומרות על התוכן הסמנטי כמו קרופ או סיבוב. ההתפלגות Q כן ידועה לנו ונרצה להיעזר בה על מנת לדגום מ- P באמצעות שיטת (importance sampling(IS. כעבור זוג דוגמאות x_i ו-x_j (שהן התמונה המקורית וגרסתה לאחר הפעלת אוגמנטציה Aj), נרצה לחשב את (P(A_j)/Q(A_j. כיוון שאנחנו לא יכולים לחשב את היחס באופן מפורש, כפי שאיננו יודעים את ההתפלגות הרצויה של אוגמנטציות P, נרצה לשערך את היחס הזה (נסמן אותו בתור w_ij). משקל w_ij ייכנס לפונקציית הלוס, וינסה לתת לאוגמנטציה הזו את המשקול ״ההולם״ עבורה ביחס לדוגמה המקורית. ככל שהאוגמנטציה שומרת יותר על התוכן הסמנטי של התמונה כך המשקל שלה יהיה גבוה יותר ואילו משקל האוגמנטציות ה״לא טובות״ יהיה קרוב ל-0. ניתן לשערך את הערך של w_ij באמצעות מרחק (מאוד דומה למרחק Mahalanobis) של ייצוג התמונה לאחר אוגמנטציה A_j מהייצוג הממוצע zmean של M אוגמנטציות שונות של התמונה.

הישגי מאמר:

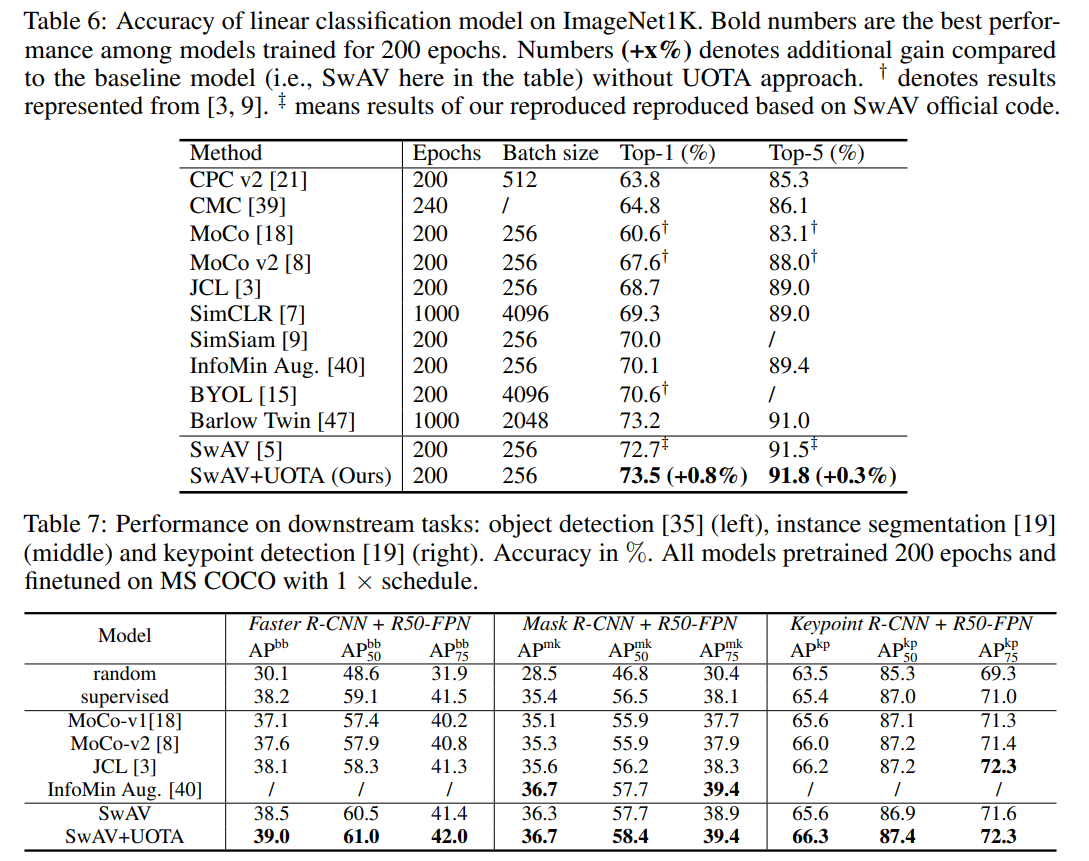
המאמר השווה אספקטים רבים של ביצועי הגישה המוצעת עם שיטות SOTA רבות, אך החשובה העיקריות ביניהם היא ההשוואת ייצוגים המופקים באמצעות הטכניקה המוצעת עם אלו של שיטות unsupervised אחרות עבור משימות סיווג וזיהוי אובייקטים. השיטה המוצעת מצליחה להשיג את הביצועים הטובים ביותר, אך השיפור על פני אלגוריתמים אחרים לא גדול.

נ.ב. 

לסיכום, מדובר במאמר מאוד מעניין המציע דרך להתמודד עם אוגמנטציות שלא משמרות את התוכן הסמנטי של תמונה במהלך למידה ייצוגית על דאטהסטים לא מתויגים.

הפוסט נכתב על ידי מיכאל (מייק) ארליכסון, PhD, Michael Erlihson ואברהם רביב.

מיכאל עובד בחברת הסייבר Salt Security בתור Principal Data Scientist. מיכאל חוקר ופועל בתחום הלמידה העמוקה, ולצד זאת מרצה ומנגיש את החומרים המדעיים לקהל הרחב.

אברהם סטודנט לתואר שלישי בתחום של למידת מכונה באוניברסיטת בר-אילן ועובד בחברת סמסונג. מתעניין בלמידה עמוקה ומגוון יישומים כולל ראייה ממוחשבת ועיבוד שפה טבעית.

מיכאל ואברהם כתבו יחד ספר על למידת מכונה ולמידה עמוקה בעברית.

ברצוננו להודות לעדו בן-יאיר על עזרה בהגהה ובחידוד של נקודות חשובות.