Geometric Dataset Distances via Optimal Transport

סקירה זו היא חלק מפינה קבועה בה אני סוקר מאמרים חשובים בתחום ה-ML/DL, וכותב גרסה פשוטה וברורה יותר שלהם בעברית. במידה ותרצו לקרוא את המאמרים הנוספים שסיכמתי, אתם מוזמנים לבדוק את העמוד שמרכז אותם תחת השם deepnightlearners.

לילה טוב חברים, היום אנחנו שוב בפינתנו deepnightlearners עם סקירה של מאמר בתחום הלמידה העמוקה. היום בחרתי לסקירה את המאמר שנקרא:

Geometric Dataset Distances via Optimal Transport

פינת הסוקר:        

       המלצת קריאה ממייק: חובה למתעניינים בשיטות של domain adaptation.

       בהירות כתיבה: בינונית.

      רמת היכרות עם כלים מתמטיים וטכניקות של ML/DL הנדרשים להבנת מאמר: נדרשת היכרות בסיסית עם שיטות domain adaptation והבנה טובה בכל מה שקשור לטרנספורט האופטימלי.

      יישומים פרקטיים אפשריים: מציאת זוגות של דאטהסטים ״נוחים״ לביצוע domain adaptation של מודלים ביניהם.

פרטי מאמר:

      לינק למאמר: זמין להורדה

      לינק לקוד: לא נמצא בארקיב

      פורסם בתאריך: 07.02.20, בארקיב

      הוצג בכנס: NeurIPS2020

תחום מאמר:

• אדפטציה בין דומיינים (domain adaptation)
• חקר של דמיון בין דאטהסטים
• transfer learning 

כלים ומושגים מתמטיים במאמר:

• הטרנספורט האופטימלי (optimal transport)
• מרחק וסרשטיין (WD)
• נוסחת רובינסטיין-קנטורוביץ
• שיטת Sinkhorn לחישוב OT

תמצית מאמר: 

המאמר הנסקר מציע שיטה למדידת "דמיון" (מרחק) בין דאטהסטים מתויגים. המאמר טוען כי שלמרחק המוצע קורלציה גבוהה למידת הצלחה של domain adaption בין דאטהסטים. למשל נניח שלקחנו מודל מאומן על הדאטהסט הראשון וכיילנו אותו (fine-tuning) על הדאטהסט השני. ככל שהמרחק המוצע בין הדאטהסטים קטן יותר, הביצועים של המודל המכויל על הדאטה מהדומיין של הדאטהסט השני, נוטים להיות טובים יותר (לטענת המאמר). בנוסף המרחק המוצע הינו אגנוסטי לסוג מודל, לא דורש אימון, לא מחייב שום דמיון בין הלייבלים בדאטהסטים ומתבסס על הטרנספורט האופטימלי (OT). 

תקציר מאמר:

אני רוצה להתחיל עם הסבר קצר על המושגים המתמטיים הנדרשים להבנת המאמר. נתחיל מ-OT – המושג המרכזי במאמר.

טרנספורט אופטימלי: 

טרנספורט אופטימלי (OT) הינו מרחק המוגדר בין שתי מידות הסתברות P ו-Q המוגדרות על אותו מרחב X לפונקציית מחיר אי שלילית (c(x,y – נוסחה (1) במאמר. נוסחה זו נראית קצת מפחיד אבל צריך לזכור שבסך הכל OT מודד עד כמה מידות הסתברות "קרובות" (כמו מרחקים KL ו-JS). המקרה הפרטי של OT שבו פונקציית מחיר הינה מרחק L_p (בין שתי נקודות x ו-y) עבור 0<p נקרא מרחק וסרשטיין מסדר p. כאשר p=1 המרחק הזה נקרא מרחק earth mover.

אז בואו נבין מה זה בעצם מרחק OT המתואר כאמור ע"י נוסחה (1) במאמר. יש בנוסחה משהו קצת מפחיד: מופיע שם איזה מינימום מעל כל מידות הסתברות (π(x,y מעל מרחב המכפלה (product) של X עם עצמו כאשר הפונקציות השוליות של π הן מידות ההסתברות שעבורן אנו מחשבים את המרחק, כלומר P ו-Q. תחת סימן האינטגרל יש לנו את המרחק בין הנקודות. כלומר מרחק OT מוגדר כמרחק הממוצע המינימלי מעל כל ההתפלגויות π האפשריות, המקיימות את התנאי מהמשפט הקודם. 

בשביל להבין את הנוסחה זו יותר טוב, בואו ניקח p=1 והמרחק האוקלידי כמטריקת המרחק c. בנוסף נניח שמרחב X הינו חד מימדי (R). למה OT נקרא מרחק Earth Mover במקרה הזה? בעצם המרחק הזה מגדיר כמה "מסה" (הסתברותית), אנו צריכים להעביר בשביל להפוך את מידת ההסתברות P ל-Q כאשר המחיר של העברת נקודה x מהתומך של P לנקודה y מהתומך של Q הוא |x -y|. עכשיו למה יש בנוסחה מינימום, אתם שואלים? כמו שאתם מבינים אפשר "להפוך P ל-Q במספר דרכים ואנחנו רוצים את הדרך הכי זולה (הדורשת העברה של כמה שפחות מסה). הדבר האחרון שנותר לנו להבין בנוסחה המגדירה את OT, הוא מידת הסתברות על מרחב המכפלה של X עם עצמו? פונקציה זו מגדירה איזה "חלק" מהמסה ההסתברותית בנקודה x מהתומך של P אנו מעבירים לנקודה y מהתומך של Q. לדוגמא אם יש ל-x הסתברות 0.5 אנו יכולים להעביר שליש ממנה (0.5*⅓  ~= 0.16) לנקודה y_1 ושני שליש (0.5*2/3  ~= 0.33) לנקודה  y_2 מהתומך של Q. התנאי שהפונקציות השוליות של π צריכות להיות שוות ל-P ו-Q נדרש כי אנו רוצים להעביר את כל המסה ההסתברותית מכל הנקודות מהתומך של P לכל הנקודות מהתומך של Q בלי לאבד (או להרוויח) מסה.

הערה לגבי OT: להבדיל כמעט מכל מרחק בין מידות הסתברות, מרחק OT (וכמובן המקרה הפרטי שלו WD) לוקח בחשבון של התכונות של הסטים שעליהם מידות אלו מוגדרות בצורה מפורשת עי" התחשבות במרחק בין הנקודות שלהם. 

מציאת מרחק וסרשטיין:

למרות האינטואיטיביות הרבה שיש בהגדרה של OT ו-WD בפרט, מציאתם אינה טריוויאלית ברוב המקרים. עבור p=1 ניתן להשתמש (כמו שעשו ב-Wasserstein GAN) בתצוגה הדואלית של בעיית אופטומיזיה המגדירה אותה (שוויון רובינשטיין – קנטורוביץ – RK). במקום לחשב את המינימום על מידות הסתברות מעל מרחב המכפלה, RK מחפשת למקסם את הפרש התוחלות של h מעל P ומעל Q כאשר h היא פונקציות ליפשיץ עם מקדם 1.

אולם במקרה שלנו גם בעיית האופטימיזציה הדואלית היא רחוקה מלהיות פשוטה לפיצוח. במקרה של שני דאטהסטים בגודל סופי ניתן להגדיר את מידות ההסתברות על המרחבים שלהם כסכום של פונקציות דלתא על הנקודות (דוגמאות) של הדאטהסטים. מרחק בין נקודות בדאטהסטים ניתן להגדיר באמצעות מטריצה כאשר איבר (i,j) שלה הוא מרחק בין נקודה x_i מהדאטהסט הראשון לבין y_j מהדאטהסט השני. ניתן לראות כי בעיית אופטימיזציה (המקורית) עבור WD הופכת לבעיית תכנות לינארי במקרה הזה. ד"א מידת הסתברות על מרחב המכפלה π שעליה מבצעים אופטימיזציה ניתנת לתיאור באמצעות מטריצה גם כן. עדיין לדאטהסטים גדולים הפתרון של בעיית תכנות לינארי זאת דורש משאבי חישוב אדירים ולא feasible. ב-2013 Sinkhorn הציע להוסיף לבעיה זו איבר רגולריזציה המודד מרחק KL בין π לבין המכפלה הקרטזית של P ו-Q. תוספת זו איפשרה לפתור את הבעייה בצורה יותר יעילה.

מרחק בין דאטהסטים דרך מרחק וסרשטיין:

נחזור כעת לבעיה שלנו ונראה איך מגדירים את מרחק בין דאטהסטים באמצעות כל המושגים שהגדרנו. קודם כל נציין כי מידת ההסתברות עבור דאטהסט מתויג מוגדרת על מרחב Z שהוא המכפלה הקרטזית של מרחב הפיצ'רים ומרחב הלייבלים. ד״א מרחבי הלייבלים אינם חייבים להיות זהים עבור שני הדאטהסטים, אך נניח זאת כאן לפשטות ההסבר. המאמר מציע להגדיר את המרחק בין שתי דוגמאות: (z_1 = (x_1, y_1 ו-(ֿz_2 = (x_2, y_2 כסכום של המרחקים בין x_1 ל-x_2 (השייכים לדאטהסט הראשון והשני בהתאמה) ולבין y_1 ל-y_2 במרחב הלייבלים. בעצם המרחק מוגדר כשורש p מהסכום של חזקות p של המרחקים מהמשפט הקודם.

אז המרחק בין הפיצ'רים (המרחק הראשון) מחושב בצורה ישירה (אוקלידי או כל מרחק מתאים אחר). המרחק בין הלייבלים קצת יותר בעייתי. הדבר הפשוט ביותר הוא לתאר כל לייבל כממוצע של הפיצ'רים של כל הדוגמאות נושאות הלייבל הזה אך זה לא מספיק מייצג את הלייבל. הדרך היותר טובה היא לחשב אותה כמרחק וסרשטיין בין ההתפלגויות המותנות של פיצ'רים בהינתן הלייבלים. עם המרחק בין z_1 ו-z_2 מוגדר כך, ניתן להוכיח שזה מטריקת מרחק תקינה, וגם מוגדרת על סטים דיסקרטיים כמו שאנחנו צריכים. בסוף המרחק בין הדאטהסטים מוגדר (בדומה ל-OT) כמינימום על כל מידות מכפלה על Z עם עצמו. את הבעייה הזו ניתן לפתור עם הוספת איבר רגולריזציה KL כמו שהזכרתי קודם. לצערנו אפילו לפתרון הזה יש סיבוכיות (n^5*log(n (כאשר n הוא גודל הדאטהסט) שהופך אותו ללא ישים לדאטהסטים גדולים. במקום זאת המחברים מציעים לשערך את ההתפלגות המותנית של פיצ'רים בהינתן לייבל באמצעות גאוסיאנים שעבורם קיים ביטוי סגור עבור WD. סיבוכיות החישוב במקרה הזה יורדת ל-n^2. המאמר גם מוכיח כי המרחק המוצע עם שערוך גאוסיאני זה חסום עי״ המרחק המקורי מלמעלה.

הישגי מאמר:

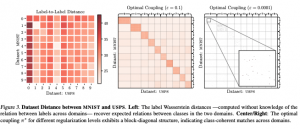
עבור מגוון זוגות של דאטהסטים המאמר משווה את הפרשי השגיאה על טסט סט של המודל עבור הדאטהסט השני בין שני תרחישים: אימון רגיל מאפס מול אימון של הראשון וכיול של השני (מאותחל עם המשקלים של הראשון). המחברים מראים שככל שהמרחק המוצע בין דאטהסטים קטן יותר, הירידה ההפרש קטן יותר כלומר יותר דמיון (מרחק קטן יותר) בין דאטהסטים מתורגם ל״רמת הצלחה״ בכיול של מודל מהדאטהסט הראשון לשני.

דאטהסטים: MNIST, FASHION-MNIST, KMNIST,  letters EMNIST

נ.ב.

מאמר עם רעיון מאוד מעניין. מסקרן לראות האם גישה זו תעבוד עבור דאטהסטים יותר "רציניים". נזכיר כי במרחק המתואר במאמר אין התחשבות לא בפוקציית לוס ולא בסוג המודלים שמשתשמים בהם לאחר מכן לסיווג – לי נראה תוספת של "התחשבות" כלשהי בסוג המודלים עשויה לשפר את התכונות של המרחק המוצע. מקווה שנרא הרחבות בקרוב.

#deepnightlearners

הפוסט נכתב על ידי מיכאל (מייק) ארליכסון, PhD, Michael Erlihson.

מיכאל עובד בחברת הסייבר Salt Security בתור Principal Data Scientist. מיכאל חוקר ופועל בתחום הלמידה העמוקה, ולצד זאת מרצה ומנגיש את החומרים המדעיים לקהל הרחב.