AVAE: Adversarial Variational AutoEncoder (סקירה)

סקירה זו היא חלק מפינה קבועה בה אני סוקר מאמרים חשובים בתחום ה-ML/DL, וכותב גרסה פשוטה וברורה יותר שלהם בעברית. במידה ותרצו לקרוא את המאמרים הנוספים שסיכמתי, אתם מוזמנים לבדוק את העמוד שמרכז אותם תחת השם deepnightlearners.

לילה טוב חברים, היום אנחנו שוב בפינתנו deepnightlearners עם סקירה של מאמר בתחום הלמידה העמוקה. היום בחרתי לסקירה את המאמר שנקרא: 

AVAE: Adversarial Variational AutoEncoder

תאריך פרסום: 21.12.2020

הוצג בכנס: טרם ידוע

תחומי מאמר:

• אוטו-אנקודר וריאציוני (VAE – Variational AutoEncoder).
• גאנים (GANs – Generative Adversarial Networks).

כלים מתמטיים, טכניקות, מושגים וסימונים:

• פונקצית לוס של VAE (המתקבלת מ- ELBO – Evidence Lower Bound)
• מרחק KL בין התפלגויות.
• מידע הדדי בין משתנים אקראיים/התפלגויות (Mutual Information).
• צוואר בקבוק אינפורמציוני (information bottleneck).
• פונקציית הלוס הסטנדרטית של גאן (מהמאמר המקורי) והפתרון האופטימלי שלה מבחינת הדיסקרימימטור.

בהירות כתיבה: בינונית מינוס 

רמת היכרות עם כלים מתמטיים וטכניקות של ML/DL הנדרשים להבנת מאמר: נדרשת הבנה עמוקה ב- VAE, גאנים ותכונותיהם בשביל להבין לעומק את הרעיון הבסיסי של המאמר. שליטה בכלים מתמטיים מתחום ההסתברות והסטטיסטיקה נחוצה להבנת המאמר.

יישומים פרקטיים אפשריים: גינרוט תמונות באיכות גבוהה עם VAE (סוג של 😀 ).

המלצת קריאת ממייק: מומלץ לבעלי ידע עמוק ב- VAE, גאנים ובעלי ידע מוצק בהסתברות בתור אתגר.

מבוא והסבר כללי על תחום המאמר: יצירה של תמונות פוטוריאליסטיות עי" רשתות נוירונים הפכה לנושא חם בלמידה העמיקה מאז שיאן גודפלו (Ian Goodfellow) הגה את הרעיון של GANs ב- 2014. מאז הוצעו מספר מודלים גנרטיביים שונים ליצירת דאטה במספר דומיינים שהפופולריים ביניהם הגאנים ו-VAE, כאשר לכל אחד מהם יתרונות וחסרונות משלה. למשל GAN מצטיין ביצירת תמונות שנראות ממש כמו אמיתיות (קרי פוטוריאליסטיות) אך הוא מאוד קשה לאימון. התופעות כמו Mode Collapse (יצירה של תמונות כמעט זהות עי" הגנרטור) וגם ההתכנסות של תהליך האימון אינה מובטחת – אלו רק חלק מהבעיות שעלולות לעלות במהלך אימון של גאן. בנוסף המבנה של המרחב הלטנטי של גאן אינו נוח לניתוח ולא נתון בצורה מפורשת. מהעבר שני VAEs יותר קלים לאימון והמרחב הלטנטי שלהם נתון בצורה מפורשת יותר אך התמונות שנוצרות באמצעותם הן מטושטשות ופחות פוטוריאליסטיות לרוב.

קודם כל ניזכר ממש בקצרה מה זה בעצם VAE.

הסבר קצר על VAE: ארכיטקטורה של VAE מורכבת משתי רשתות עם פרמטרים נלמדים.

• הרשת המקודדת (אנקודר) E_vae שממפה דוגמא מהמרחב המקורי למרחב הלטנטי Z (בעל מימד נמוך).
• הרשת המפענחת D_vae (דקודר) מנסה לשחזר את הדוגמא מהייצוג הלטנטי שלה. 

האימון של VAE מתבצע בצורה הבאה: 

• הרשת המקודדת E_vae ממפה דוגמא X לפרמטרים של הייצוג הלטנטי שלה z.
• מגרילים וקטור אקראי (בדרך כלל גאוסי) עם הפרמטרים מהשלב הקודם.
• מעבירים את הוקטור המוגרל דרך הרשת המפענחת D_vae לשחזור של הדוגמא המקורית X.

פונקצית הלוס של VAE, המסומנת עי״ L_vae, מתקבלת עי״ שימוש בחסם העליון של ELBO – evidence. פונקצית לוס זו מורכבת משני מחוברים: 

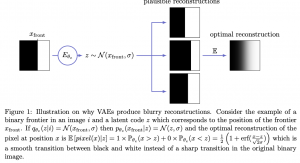
• לוס השחזור: עד כמה טוב D_vae הצליחה לשחזר את התמונה המקורית X. בדרך כלל לוס השחזור מחושב כמרחק הריבועי L_q בין התמונה בין התמונה המקורית למשוחזרת.
• מרחק KL בין התפלגות פריור על מרחב הלטנטי לבין התפלגות פוסטריור שלה (המשוערכת על סמך פלטים של הרשת המקודדת E_vae). נסמן את המרחק הזה ב L_kl.

בתהליך האימון של VAE הרשת המקודדת והרשת המפענחת מאומנות במטרה למזער את L_vae.

כדי להבין את הסיבות העיקריות ליכולת החלשה של VAE ליצור תמונות פוטוריאליסטיות, המאמר מנתח את פונקצית הלוס שלה ומציין שתי סיבות עיקריות לכך:

סיבה 1: המאמר מנתח את האיבר השני שלו, כלומר L_kl, ומוכיח שניתן לתאר את L_kl כסכום של המידע ההדדי בין הדוגמה x לייצוג הלטנטי האפוסטריורי שלה z|x, ומרחק KL בין ההתפלגות האפוסטריורית z|x והתפלגות הפריור של z (בדרך כלל גאוסי בעל תוחלת אפס מטריצת קווריאנס I). מזעור של איבר זה משמעו 

הגבלה על מידע הדדי בין דוגמא לייצוגה הלטנטי (!!) במטרה לקרב את ההתפלגות של z|x לזו של הפריור z. 

כלומר, איבר זה הינו למעשה צוואר בקבוק אינפורמציוני המגביל את זרימת המידע בין x לייצוג הלטנטי שלה. זה בפועל מקשה על הרשת המפענחת לשחזר את התמונה המקורית מהקוד הלטנטי שלה (כי חלק מהמידע הולך לאיבוד בין הדוגמא לייצוגה הלטנטי עקב צוואר הבקבוק האינפורמציוני). בנוסף הלוס הריבועי המופיע באיבר הראשון של L_vae, גורמת ל- VAE ליצור תמונות מטושטשות. המאמר מצטט עבודה של LeCun et al המראה שלמעשה הערך האופטימלי של כל פיקסל בתמונה המשוחזרת הינו לו התוחלת שלו המותנית ב״מידע הנמצא בקוד הלטנטי שלה״. כתוצאה מכך הרשת המפענחת לרוב פשוט לא מצליחה להפיק תמונה פוטוריאליסטית מהייצוג החלקי שמוזן אליה. 

סיבה 2: הסיבה השנייה טמונה בהנחה המקובלת בראייה הממוחשבת כבר שנים: לתמונות הטבעיות יתירות רבה (במיוחד היתירויות הלוקאליות) שמאפשרת לתאר אותן במרחב ממימד נמוך (low-dimensional manifold). אולם (לטענת המאמר) הטקסטורות כמו עץ, שער או גלים אינם ״חיים״ במניפולד ממימד נמוך, עקב התכונות האינהרנטיות שלהם (למשל שיער של אדם מורכב מהרבה שערות שלכל אחד אופיינים משלו). לעומת VAE, הגאנים מצליחים להתגבר חלקית על סוגיה זו ע"י יצירה של דוגמאות המהוות תת-קבוצה של המניפולד ממימד גבוה שבו "חיות" הטקסטורות, שמספיקות כדי "להוליך שולל" את הדיסקרימינטור. כתוצאה מכך התמונות של גאן יוצאות יותר "טבעיות" ופחות מטושטשות של VAEs.

רעיון המאמר בגדול: המאמר מציע לשלב את היתרונות של VAE וגאנים עי״ שיבוצם בארכיטקטורה שלהם, הנקראת AVAE.  אני רוצה לציין שהרעיון הזה לא חדש וכבר ב- 2015 ניסו לעשות זאת ב- VAE/GAN. במאמר הציעו להחליף את השגיאה הריבועית ברשת המפענחת בדיסקרימינטור כמו זה של גאן.  הבעיה בגישה הזו שהדמיון של התמונה המשוחזרת למקורית כבר לא בא לידי ביטוי. שיטה יותר מפורסמת המשלבת את שתי גישות אלו (VAE חלקית וגאן) הינה BiGAN שמורכב מהרשת המקודדת, הרשת המפענחת והדיסקרימינטור. הדיסקרימינטור מנסה להבחין לא רק בין התמונות המגונרטות לאמיתיות אלא גם בין הווקטורים הלטנטיים שנדגמים המפריור לבין לאלו שנוצרים עי״ הרשת המקודדת. BiGAN מצליח ליצור תמונות פוטוריאליסטיות אך (לטענת המאמר) יכולת השחזור שלו נמוכה (כלומר תמונות נוצרות מוקטורים קרובים לייצוג לטנטי של תמונה נתונה x, לא תמיד יוצאות דומות ל- x), כלומר המרחב הלטנטי פחות קוהרנטי. 

המאמר הנסקר מציע לשלב את לוס השחזור עם הלוס האדוורסרי בצורה שתיצור גם תמונות באיכות דומה בלי לפגוע ב״קוהרנטיות של המרחב הלטנטי״. הרעיון העיקרי של AVAE הינו הוספת רשת הגנרטור G ל- VAE הסטנדרטי, שלוקחת כקלט את הווקטור הלטנטי המופק עי״ הרשת המקודדת E_vae. המאמר גם מציע להוסיף(concatenate) לקלט של G וקטור נוסף z_a המפולג עם התפלגות גאוסית סטנדרטית – לטענת המאמר z_a מיועד לייצוג מידע מתמונה שהרשת E_vae לא הצליחה להפיק ממנה. 

הסבר מעמיק על רעיונות בסיסיים: 

נתחיל מההסבר על פונקצית לוס L_avae של AVAE. פונקצית הלוס של AVAE הינה סכום (משוקלל) של הלוס הסטנדרטי של VAE, המסומן כ- L_vae והלוס של הגנרטור G, המסומן ב- L_G. עקרונית הגנרטור G צפוי לשרת כ"הופכית" של הרשת המקודדת E_vae וזה הנקודה החשובה של המאמר:

ההתפלגות המותניתp_G(x|z) של פלט הגנרטור G בהינתן וקטור לטנטי z והתפלגות p_enc(x|z) של פלט(!!) הרשת המקודדת, בהינתן וקטור הלטנטי  z,, צריכות להיות כמה שיותר קרובות (כאשר הווקטור z מתפלג לפי התפלגות הפריור).

כלומר פונקצית המטרה L_G של הגנרטור G הינה הקרוס-אנטרופי בין p_enc(x|z) לבין p_G(x|z) כלומר התוחלת של -log(p_enc(x|z)) מעל ההתפלגות p_G(x|z), כאשר z מתפלג לפי התפלגות הפריור (N(0, I.

הערת צד לגבי האימון: במהלך האימון של AVAE, הקלט של G אינו נלקח מהפלט של הרשת המקודדת E_vae , אלא נדגם ישירות מהתפלגות הפריור של z. אני מנחש שזה הופך את הגנרטור יותר דומה לזה של הגאן המקורי במטרה ״לחקות״ את תכונות החזקות שלו ביצירה פוטוריאליסטיות.

נתחיל מקצת אינטואיציה מאחורי הרעיון הדי לא טריוויאלי הזה:

פינת אינטואיציה: שימו לב שהמטרה כאן היא לאמן את הגנרטור ליצור תמונות פוטוריאליסטיות מהתפלגות הפריור מחד (נראה בהמשך איך LG מוביל ללוס דומה לזה של הגאן הסטנדרטי) עבור וקטורים לטנטיים המתפלגים לפי הפריור הנתון. שנית זה ״מאלץ״ את הרשת המקודדת להפיק פיצ'רים לטנטיים הנחוצים ליצירת תמונה פוטוראליסטית. שלישית L_vae מאלץ את הרשת המקודדת E_enc להפיק פיצ'רים הנחוצים לשחזור מדויק של התמונה (עי״ מזעור המרחק הריבועי בין התמונה המקורית למשוחזרת). המשחק המורכב הזה מאפשר ל- G ליצור תמונות פוטוריאליסטיות מחד תוך שמירת קוהרנטיות של המרחב הלטנטי (וקטורים לטנטיים קרובים יוצרים תמונות דומות כלומר ״יחסי המרחק״ במרחב המקורי ובמרחב הלטנטי נשמרים). 

עכשיו בואו נבין איך L_G מוביל ללוס דומה לזה של גאנים ״הגורם״ לו ליצור תמונות פוטוריאליסטיות. המאמר מוכיח ש- L_G ניתן לפירוק לסכום של המחוברים הבאים:

• האיבר הראשון: תוחלת של (log(p_enc(z|x_G) מעל ההתפלגות (p_G(x|z כאשר הווקטור z מתפלג לפי התפלגות הפריור. איבר זה למעשה משערך עד כמה ״סביר״ להפיק וקטור לטנטי z מהתמונה דרך הרשת המקודדת E_vae, כאשר x_G שנוצר עי״ הגנרטור G בהינתן אותו וקטור לטנטי z. החלק הזה הוא קל יחסית לחישוב – ומשוערך כמרחק ריבועי בין z לבין התוחלת של הפלט ש- E_vae מפיק מ- x_G, מנורמל בשונות של הפלט שלו. נזכיר שבהינתן תמונה x המקודד מוציא זוג של ( mu_enc(x), sigma_enc(x)) של התוחלת והשונות של הייצוג הלטנטי של x בהתאמה (מהם מגרילים את הקלט לרשת המפענחת D_vae).
• האיבר השני: מרחק KL בין ההתפלגות p_G(x) לבין ההתפלגות האמיתית של הדאטה p_data(x). כאן נכנס הקטע של הלוס האדברסריאלי. כדי לשערך את הלוס הזה מאמנים רשת מבקרת (critic), המסומנת כ- C, שמטרתה להבחין בין התמונות האמיתיות מהדאטהסט לאלו שנוצרו עי״ הגנרטור  (הפלט של הינו הסתברות של הקלט להיות תמונה אמיתית). פונקצית המטרה של C הינה זהה לפונקצית המטרה סטנדרטית של גאן L_GAN. אבל איך כל זה למעשה קשור למרחק KL בין p_G(x|z) לבין p_data(x), אתם שואלים? אולי אתם זוכרים שהפתרון האופטימלי עבור L_GAN מבחינת הרשת המבקרת C לרשת הגנרטור נתונה, הינו היחס בין p_G(x) לבין הסכום של p_data(x) ו- p_G(x). אם נציב את הפתרון הזה לפונקציית המטרה L_gan נקבל את הלוגריתם של היחס בין p_G(x) לבין p_data(x) המהווה משערך בלתי מוטה למרחק KL בין p_G(x) לבין p_data(x). כלומר אם נאמן את C מספיק טוב ונציב אותו ל L_gan עבור תמונה x נתונה הערך המתקבל יכול לשמש כמשערך לאיבר השני של הלוס L_G.
• האיבר השלישי: אנטרופיה של p_G(x) (התפלגות התמונות הנוצרות עי״ הגנרטור). איבר זה אינו תלוי בדאטה (מתאר את ההתפלגות הפלט הגנרטור). מינימיזציה של איבר זה מאלצת את p_G(x) להיות יותר מרוכזת סביב המודים שלה (זה גורם לירידה באנטרופיה) והמאמר מציע לא לקחת אותו חשבון כאמצעי רגולריזציה (נציין שהאיבר הזה הינו intractable)

לסיכום, AVAE מורכב מ 4 הרשתות הבאות: 

• הרשת המקודדת הסטנדרטית E_vae
• הרשת המפענחת הסטנדרטית D_vae. 
• הגנרטור G המיועד ליצירת תמונה מוקטור לטנטי (עם אופציה להוסיף וקטור לטנטי נוסף לכיסוי של תכונות של תמונות ש- E_vae לא הצליחה להפיק)
• הרשת המבקרת (דיסקרימינטור) C שמטרתה להבחין בין התמונות מהדאטהסט לתמונות מגונרטות

המפלצת הזו מאומנת עם פונקציית מטרה שהיא סכום של L_vae ו- L_G שמוסברים מעלה.

הישגי מאמר: המאמר משווה את ביצועיו של AVAE מול השיטות הבאות: VAE, VAE/GAN, BiGAN ומשתמש ב 3 מטריקות: לוס השיחזור הריבועי, LPIPS ו- FID על הדאטהסטים הבאים:

• Bedroom
• CelebA
• CIFAR10
• CIFAR100
• SVHN

עבור כמה מהדאטהסטים האלו הם הצליחו להשתפר בחלק מהמטריקות (הלוס הריבועי שופר עבור כל הדאטהסטים) אבל רוב השיפורים לא נראים לי ממש מרשימים. הם גם טוענים שהתמונות שלהם נראות יותר פוטוראליסטיים מאלו של VAEs אחרים ואני נוטה להסכים איתם אך זה די סובייקטיבי 🙂

לינק למאמר: זמין להורדה

לינק לקוד: למרות שבמאמר מופיע שהקוד יהיה זמין בגיטהאב לא הצלחתי לאתרו.

נ.ב. מאמר עם רעיון מאוד מעניין ומגניב אך כתוב בצורה לא מספיק ברורה. תרשימי זרימה שיש במאמר לרוב לא עוזרים בהבנה. צריך להודות שהתוצאות לא הרשימו אותי יותר מדי וגם הקוד לא שותף שזה די מאכזב. נאלץ לא להעניק לו המלצת קריאה ממייק. עם זאת הכלים/תובנות המתמטיים שפותחו במאמר נראים לי מבטיחים ומעניינים ואני מקווה לראותם מיושמים בעתיד ומשיגים תוצאות משמעותיות יותר.

#deepnightlearners