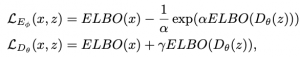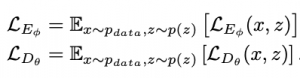Soft-IntroVAE: Analyzing and Improving the Introspective Variational AutoEncoder, סקירה

סקירה זו היא חלק מפינה קבועה בה אני סוקר מאמרים חשובים בתחום ה-ML/DL, וכותב גרסה פשוטה וברורה יותר שלהם בעברית. במידה ותרצו לקרוא את המאמרים הנוספים שסיכמתי, אתם מוזמנים לבדוק את העמוד שמרכז אותם תחת השם deepnightlearners.

לילה טוב חברים, היום אנחנו שוב בפינתנו deepnightlearners עם סקירה של מאמר בתחום הלמידה העמוקה. היום בחרתי לסקירה את המאמר שנקרא: 

Soft-IntroVAE: Analyzing and Improving the Introspective Variational AutoEncoder

פינת הסוקר:  

      המלצת קריאה ממייק: מומלץ לאוהבי מודלים גנרטיביים 

      בהירות כתיבה: גבוהה.

     ידע מוקדם: 

• הבנה של עקרונות VAE (למשל שימוש ב- ELBO לשערוך של הנראות המירבית).
• עקרונות אימון של מודלים גנרטיביים עם פונקציית לוס אדוורסארית (משחק mini-max כמו בגאן) – נא לא לבלבל שיטות אלו עם שיטות לאימון רשתות ״חסינות״ נגד התקפות אדוורסריות (adversarial examples).
• ידע בהסתברות אם אתם רוצים להבין את הפרקים עם ההוכחות.

   יישומים פרקטיים אפשריים: יצירה (אינפרנס) של תמונות באיכות גבוהה בסיבוכיות חישובית של VAE רגיל.

פרטי מאמר:

      מאמר: זמין להורדה.

      קוד: כאן

      פורסם בתאריך: 25.03.21, בארקיב.

      הוצג בכנס: CVPR 2021.

תחומי מאמר:

• מודלים גנרטייביים ליצירת דאטה ויזואלי (תמונות)

כלים מתמטיים, מושגים וסימונים:

• ELBO
• VAE(Variational AutoEncoder)
• אימון מודלים גנרטיביים עם פונקציית לוס אדוורסרית 

מבוא:

היום אני סוקר עוד מאמר המציעה גישה לשיפור של איכות התמונות הנוצרות באמצעות מודל גנרטיבי מסוג VAE. אחת נקודת התורפה של VAE היא הקושי שלהם לגנרט תדרים גבוהים הנובע בין השאר ממבנה של איבר השחזור (reconstruction term) המופיע בפונקציית הלוס שלה. איבר השחזור מכיל מרחק L2 בין התמונה המקורית למשוחזרת, המתקבלת באמצעות העברת התמונה המקורית דרך האנקודר והדקודר. מזעור איבר זה גורם לתמונות המשוחזרות להיות דומות למקוריות ״בממוצע״ שמתבטא ביצירת תמונות בעלות אזורים חלקים ונטולי פרטים (תדרים גבוהים). ניתן לנסח את הבעיה באופן הבא: VAE יודע "לתת" הסתברויות גבוהות לדגימות אמיתיות, אך מתקשה "לתת" הסתברויות נמוכות לדגימות מטושטשות. מכיוון שגאנים מודרניים כבר לא סובלים מבעיה זו (יש לגאנים חסרונות אחרים כמו מוד קולפס ואימון לא יציב) אז נראה לכאורה ששילוב של גאן ו-VAE עשוי לתת מענה לסוגיית התדרים הגבוהים של VAE.

בסקירתי האחרונה תיארתי מודל שהוא שילוב של VAE וגאן, הנקרא VQ-GAN. המאמר הנסקר אז הציע להוסיף ל-VAE רשת הדיסקרימינטור D במטרה להבחין בין התמונה המקורית לבין התמונה המשוחזרת (בדומה לגאנים). כלומר המחברים "הוסיפו גאן" ל- VAE כאשר רשת הדקודר משחקת תפקיד של גנרטור של גאן. שילוב של הלוס האדוורסרי הסטנדרטי של גאן בפונקציית לוס של VQ-GAN הצליח להתגבר על בעיית ה״תדרים הגבוהים״ בתמונות הנוצרות. למעשה רשת הדיסקרימינטור מאומנת להבחין בין התמונות המשוחזרות לבין המקוריות וזה מאפשר ל- VQ-GAN לגנרט תמונות פוטוריאליסטיות מדהימות.

תמצית מאמר:

כמובן שהוספת רשת נוספת ל-VAE מקשה על האימון של VQ-GAN. זה מוביל אותנו לשאלה הבאה: האם ניתן להשיג את היתרון של הלוס האדוורסרי של גאן מבלי לשנות את המבנה המקורי של VAE? מתברר שהתשובה על השאלה הזו היא חיובית וזה בדיוק מה שעשה המאמר שאסקור הפעם. 

המאמר הנסקר מציע שיטה שכלשונו מאפשרת "לאמן את VAE בצורה introspective, כלומר VAE עצמו מאומן לחפש הבדלים בין תמונות מגונרטות באמצעותו לבין התמונות המקוריות". כדי לעשות זאת רשת האנקודר לובשת כובע של הדיסקרימינטור, כאשר הדקודר משחק תפקיד של הגנרטור. בפרק הבא נתאר איך ניתן לבנות פונקציית לוס המשלבת את הלוס האדוורסרי של גאן עם הלוס של VAE.

תקציר מאמר:

כעת נתאר את המבנה של פונקציית לוס של Soft-IntroVAE. קודם כל נציין שהמאמר הנסקר הוא שיפור של מאמר, המציע מודל בשם IntroVAE שלראשונה הצליח להכניס גאן ל-VAE ללא תוספת של רשתות נוספות. 

נתחיל מתיאור של פונקציית לוס של IntroVAE. להבדיל מ- VQ-GAN ״ההבחנה״ בין תמונות מגונרטות למקוריות נעשית לא במרחב המקורי (של תמונות) אלא במרחב הלטנטי. הרעיון העיקרי של IntroVAE הוא לבנות משחק מיני-מקס בין הדיסקרימינטור (שזה למעשה אנקודר E) לגנרטור (אשר בנוי כדקודר אבל כאן נקרא G) כאשר:

• דיסקרימינטור מצד אחד מנסה למזער את מרחק KL בין התפלגות הייצוגים הלטנטיים של תמונות מקוריות לבין הפריור (בדרך כלל גאוסי איזוטרופי עם מטריצת קווריאנס cI). מצד שני הוא מנסה להגדיל את מרחק DL בין התפלגות הייצוגים הלטנטיים של התמונות המגונרטות לבין התפלגות הפריור. 
• גנרטור מצידו ינסה ״לקמבן״ את הדיסקרימינטור תוך מזעור של מרחק DL בין התפלגות הייצוגים הלטנטיים של התמונות המגונרטות לבין התפלגות הפריור.

אוקיי, אבל איך זה נעשה בפועל. איך ניתן לשלב בין הלוס הרגיל של VAE לבין הלוס האדוורסרי שמוגדר למעלה? האמת שהמאמר בחר בגישה די אינטואיטיבית. פונקציית לוס של האנקודר (דיסקרימינטור) מורכבת מסכום של L_E ו- L_G כאשר:

L_E: הלוס הרגיל של VAE (למעשה זה הלוס של β-VAE כאשר איבר KL בא עם מקדם β) ומרחק KL בין התפלגות הפריור (p(z לבין ייצוגים לטנטיים של תמונות מגונרטות. מתמטית הלוס נראה באופן הבא:

כאן:

1. L_REG( z_g) מסמן מרחק KL ממוצע (על פני תמונות מהדאטהסט) בין התפלגות של וקטור z_g המוווה ייצוג לטנטי של תמונה משוחזרת לבין התפלגות פריור של וקטור לטנטי של תמונה מהדאטהסט (כלומר התפלגות גאוסית N(0,cI)).שימו לב כי בביטוי עבור L_E מופיע סכום של L_REG(z_r) ו- L_REG(z_p) כאשר z_r ו- z_p הינם ייצוגים לטנטיים של תמונות מגונרטות באמצעות האנקודר המתקבלות באופן קצת שונה – הסבר לגביהם יינתן בהמשך.
2. L_AE(x, x_r) הוא לוס השחזור בין תמונה x לבין גרסתה המשוחזרת x_r.
3. α, β ו- m הם הייפר-פרמטרים ו- ⁺[x] =: max(0, x)

L_G: מורכב מסכום של לוס השחזור ואותו מרחק KL בין התפלגות ייצוגים של תמונה מגונרטת לבין התפלגות פריור.

כאן Enc(x_s) מסמן את התוצאה של העברת התמונה x_s באנקודר.

המאמר מציע שתי דרכים לבנייה של ייצוגים לטנטיים z_r ו- zp של תמונות מגונרטות:

1. לוקחים תמונה משוחזרת x_r (לאחר העברתה של תמונה מהדאטהסט דרך האנקודר ואת התוצאה דרך דרך הדקודר) ומזינים אותה לאנקודר כדי לבנות את הייצוג הלטנטי z_r. 
2. דוגמים מהפריור (p(z וקטור z ומעבירים אותו דרך הדקודר ולאחר מכן דרך האנקודר ויוצרים ייצוג לטנטי z_p. 

כעת נדון בחולשה המרכזית של IntroVAE שאותה Soft-IntroVAE בא לתקן. המחברים של המאמר הנסקר טוענים כי אימון של IntroVAE עלול לסבול מאי-יציבית עקב רגישותו הרבה לבחירת פרמטר m (מהלוס LE). בנוסף, הניתוח התאורטי של משחק מינמקס שהוצג ב- IntroVAE לא לקח בחשבון חלק מהאיברים של פונקציית הלוס והסתפק רק בניתוח של איברים המכילים מרחקי KL.

כדי להתגבר על הקושי, הם מציעים להחליף את מרחק KL מהלוסים L_E ו- L_G לביטוי המלא של ELBO עבור התמונה המגונרטת. כלומר פונקציות לוס עבור הדיסקרימינטור (אנקודר) והגנרטור (דקודר) מקבלות את הצורה הבאה:

כאשר D_θ(z) :=p_θ(x|z) כלומר התפלגות אפוסטריורית של תמונה x בהינתן התפלגות של ייצוג לטנטי z, ו- α, γ הם שני הייפר-פרמטרים חיוביים. שימו לב כי משוואה זו מבטאת את ה״משחק״ בין האנקודר ודקודר כאשר בדומה ל- IntroVAE: 

• האנקודר מאומן להבחין בין תמונות אמיתיות (ELBO נמוך) לתמונות הנוצרות באמצעות הדקודר (ELBO גבוה),
• הדקודר מנסה ״לעבוד על״ האנקודר ומנסה לגנרט פיסות דאטה כמה שיותר משכנעות.

מבחינה מתמטית פונקציית הלוס של Soft-IntroVAE מקבלת את הצורה הבא:

כאשר p_data היא התפלגות של דאטה אמיתי ו- p(z) הינה התפלגות פריור גאוסית איזוטרופית. מעניין כי להבדיל מ- IntroVAE, המשחק בין האנקודר לדקודר מחושב במרחב המקורי של הדאטה (תמונות) ולא במרחב הלטנטי. בעיית אופטימיזציה זו פותרים בדומה ל-VAE הרגיל באמצעות Gradient Descent וטריק רפרמטרזיציה (reparametrizarion trick).

שימו לב כי הנוכחות של האיבר (exp(ELBO(D_θ(z)) בביטוי של בעיית האופטימיזציה של האנקודר, משעמותו מינימיזציה של ELBO עבור דגימות המגונרטות באמצעות הדקודר. ניזכר כי ELBO(D_θ(z)) מהווה חסם תחתון על הנראות המירבית של D_θ(z) (תמונות מגונרטות). כלומר מינימיזציה של ELBO(D_θ(z)) עלולה לפגוע ב-״איכות״ של התמונות המגונרטות. 

אם זה אכן המקרה, זה כמובן מאוד בעייתי. אז בואו נבין מה קורה כאן? קודם כל המאמר מוכיח כי שיווי משקל של נאש של בעיית האופטימיזציה של Soft-IntroVAE פותר מתכנס ל- ^*d כאשר:

כאשר H(q) היא פונקציית האנטרופיה של התפלגות q. כלומר עבור 0 ≠ γ הפתרון אינו מתכנס להתפלגות של הדאטה p_data אלא מהווה פתרון של בעיית אופטימיזציה עם איבר רגולריזציה שמעודד פתרונות בעלי אנטרופיה גבוהה מספיק. אבל האם זה טוב? המאמר טוען כי:

“Soft-IntroVAE learns distributions with sharper supports than a standard VAE, but without negative effects such as mode dropping”

על כמה דאטסטים פשוטים (toy datasets). על הדאטהסטים של תמונות ניתן לראות כי איכות התמונות המגונרטות מאוד גבוהה והתמונות עצמן די מגוונות.

מימוש: המאמר השתמש במודיפיקציה של ELBO שהוצע ב- β-VAE.

הישגי מאמר: 

המחברים הראו כי הגישה המוצעת מצליחה להשיג ביצועים יותר טובים מכמה שיטות גנרטיביות אחרות כמו StyleALAE, GLOW, Balanced Pioneer וכמה אחרים על שני דאטהסט CelebA-HQ ומראה תוצאות קרובות לגאנים עבור דאטהסט FFHQ. כמובן הגאנים עדיין מנצחים את השיטות המבוססות VAE…

נ.ב. 

מאמר עם רעיון מעניין, יש ניתוח מתמטי רציני של המודל, איכות התוצאות מרשימה. חסרות לי השוואות ביצועים עם עוד מודלים חזקים מבוססי VAE עבור דומיינים נוספים. אבל בסך הכל המאמר מומלץ בחום!

מילות תודה:  ברצוני להודות לעידו בן-יאיר על העזרתו בכתיבת סקירה זו.

#deepnightlearners

הפוסט נכתב על ידי מיכאל (מייק) ארליכסון, PhD, Michael Erlihson.

מיכאל עובד בחברת הסייבר Salt Security בתור Principal Data Scientist. מיכאל חוקר ופועל בתחום הלמידה העמוקה, ולצד זאת מרצה ומנגיש את החומרים המדעיים לקהל הרחב.