Discriminator Rejection Sampling (סקירה)

סקירה זו היא חלק מפינה קבועה בה אני סוקר מאמרים חשובים בתחום ה-ML/DL, וכותב גרסה פשוטה וברורה יותר שלהם בעברית. במידה ותרצו לקרוא את המאמרים הנוספים שסיכמתי, אתם מוזמנים לבדוק את העמוד שמרכז אותם תחת השם deepnightlearners.

לילה טוב חברים, היום אנחנו שוב בפינתנו deepnightlearners עם סקירה של מאמר בתחום הלמידה העמוקה. היום בחרתי לסקירה את המאמר שנקרא: 

Discriminator Rejection Sampling

פינת הסוקר:  

       המלצת קריאה ממייק: חובה לאוהבי גאנים ודי מומלץ עבור האחרים. 

       בהירות כתיבה:  בינונית פלוס.

      רמת היכרות עם כלים מתמטיים וטכניקות של ML/DL הנדרשים להבנת מאמר: הבנה בשיטות אימון של גאנים, ידע בסיסי בשיטות דגימה כמו Rejection Sampling.

     יישומים פרקטיים אפשריים: גנרוט תמונות יותר איכותיות עם גאנים.

פרטי מאמר:

    לינק למאמר: זמין להורדה.

    לינק לקוד: לא אותר.

    פורסם בתאריך: 26.02.19, בארקיב.

    הוצג בכנס: ICLR 2019.

תחום מאמר:

• חקר שיטות גנרוט דוגמאות באמצעות גאנים מאומנים.

כלים מתמטיים, מושגים וסימונים:

• גאנים (GANs).
• Rejection Sampling.
  

  ---

תמצית מאמר:

המאמר מציע שיטה לשיפור איכות התמונות המגונרטות על ידי GAN מאומן תוך כדי ניצול ״המידע״ שנצבר בדיסקרימינטור (D) במשך תהליך אימון של GAN. נזכיר ש-D מאומן להבחין בין תמונות המגונרטות על ידי הגנרטור G לבין התמונות מסט האימון. הפלט של D הינו הסתברות שהקלט שלו הוא תמונה אמיתית (מסט האימון). המאמר מציע לנצל את ההתפלגות על מרחב התמונות המושרית על ידי D (באופן לא מפורש) בשביל לתקן את התפלגות התמונות המושרית על ידי G (התמונות המגונרטות) ובכך לשפר את האיכות של התמונות המגונרטות.

רעיון בסיסי: 

כאשר D מאומן טוב מספיק, הוא משרה  התפלגות על מרחב התמונות בעלת התכונות הבאות:

• תמונות "שנראות דומות לטבעיות״ מקבלות הסתברויות גבוהות. 
• תמונות שנראות ״לא אמיתיות״ מקבלות הסתברויות נמוכות.

בעיקרון הרבה יותר הגיוני לדגום מההתפלגות המושרית עי״ D כי אז אנו נדגום תמונות, שנראות דומות לאמיתיות (אלו ש-D מעניק להם הסתברות גבוהה), בסבירות יותר גבוהה. אבל איך נוכל לדגום מההתפלגות הזו אם היא לא ניתנת לנו בצורה מפורשת (intractable)? כדי להתגבר על קושי זה, מחברי המאמר משתמשים בדגימות של G ומפעילים טכניקת דגימה הנקראת (rejection sampling (RS בשביל לדגום מההתפלגות המושרית על ידי D.

תקציר מאמר:

כאשר מסתכלים על הרעיון הזה בצורה מעמיקה יותר, עולות מספר שאלות לגבי יעילותו. הרי אם היה מידע מועיל כלשהו במשקלים של D, הוא היה מועבר ל-G במהלך האימון (הרי כל הרעיון של GAN מבוסס על העברת "אינפורמציה" מ-D ל-G דרך הגרדיאנט של פונקצית הלוס של GAN). אולם  יש מספר סיבות למה בפועל לא כל האינפורמציה הנצברת ב-D מועברת בסופו של דבר ל-G.

1. ההנחות על תהליך האימון של GAN לא תמיד מתקיימות (למשל הן ל- D והן ל- G יש קיבולת סופית ולא תמיד ניתן להעביר את כל האינפורמציה מאחד לשני דרך המשקלים של רשתות אלו.
2. ייתכן שקיימים מצבים שבהם יותר קל ל-D להבדיל בין התפלגות נכונה ללא נכונה (על סמך הדגימות) מאשר למדל התפלגות נכונה ב- D.|
   
3. הסיבה הכי פשוטה: ייתכן שאנחנו לא מאמנים GAN מספיק זמן בשביל ש- G יהיה מסוגל למדל את ההתפלגות האמיתית. כלומר האימון נגמר לפני שכל האינפורמציה מ-D מועברת ל-G.

נתחיל מהסבר קצר על rejection sampling המהווה את אבן היסוד של הרעיון המוצע במאמר:

:Rejection sampling (RS)

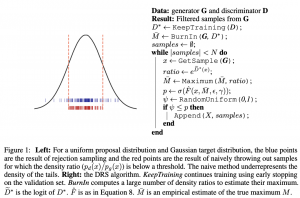
טכניקה זו מיועדת לדגימה מהתפלגויות p_d שהדגימה הישירה ממנה קשה (למשל מהתפלגות שניתנה בצורה לא מפורשת). במקום זאת דוגמים מהתפלגות אחרת p_g המוגדרת מעל אותו מרחב, שניתן לדגום ממנה, אם מתקיים התנאי הבא: המקסימום של היחס בין הערכים של p_d ושל p_g צריך להיות חסום עי" קבוע M. אז איך זה בעצם עובד? דוגמים מ-p_g נקודה y ומחשבים את הערך של p_d בנקודה y. אז מחלקים את הערך של p_d(y) ב-p_g(y) מוכפל ב-M כלומר מחשבים t=p_d(y)/Mp_g(y). ואז מקבלים את הדגימה y בהסתברות t ודוחים אותה אחרת.

נסמן ב-p_d ו-p_g  את ההתפלגויות המושרות על ידי D ו-G בהתאמה. כעת נשאלת השאלה איך אנו בעצם נבצע RS אם אנו לא יודעים לחשב לא את p_g ולא את p_d בצורה מפורשת? הטריק הוא שאנו צריכים לחשב את המנה ולא את הערכים עצמם. המאמר מציין שתחת תנאים מסוימים (״התנאים האידיאליים") על p_d ו-p_g, ניתן לדגום את pd דרך p_g בצורה מדויקת.

התנאים האידיאליים:

1. ל-p_d ול-p_g יש אותו סט תומך (כלומר הן שונות מ- 0 באותן הנקודות).
2. הקבוע M (המקסימים של היחס בין p_d ל-p_g) ידוע או וניתן לחשב אותו.
3. ל-G נתון, ניתן לאמן את D עד להבאתו לערכו המינימלי האבסולוטי התיאורטי של פונקצית הלוס של גאן (הערך הזה שווה ל-log4). כמובן שזה בלתי אפשרי כי יש לנו דאטהסטים בגודל סופי והאימון שלנו הוא גם באורך סופי.

תחת תנאים אלו המאמר מראה כי ניתן לדגום מ- p_d דרך p_g באמצעות RS. הנוסחה עבור המנה של p_d ו-p_g במקרה הזה כוללת את האקספוננט של הלוג'יט (logit) של הדיסקרימינטור האופטימלי *D (ה-D האופטימלי מוגדר בתור כזה שמביא את פונקציית הלוס למינימום האבסולוטי). ההוכחה היא די אלגנטית ומנצלת את הנוסחה עבור הערך האופטימלי של *D בנקודה x (השווה ליחס בין p_d(x) לבין p_d(x))+ (p_g(x) עבור G קבוע, המסומן על ידי D*(x). 

כמובן שאף אחד מתנאים אלו לא מתקיים במציאות. המאמר מציע דרך לבצע RS למרות אי קיום התנאים האידיאליים.  

לגבי תנאים 1) ו- 3) המאמר טוען כי ניתן להשתמש ב-D מאומן מספיק טוב כקירוב טוב של *D. אם מאמנים את D בצורה "המונעת" overfitting (רגולריזציה, עצירה מוקדמת וכדומה -לשון המאמר). במקרה זה D המאומן יודע להבדיל בין דגימה "טובה" לדגימה רעה גם אם הדגימות האלו יהיו בעלות הסתברות 0 עבור pd האופטימלי (עבור *D). הם גם מוכיחים הנחה זו אמפירית.

לגבי 2) הם מציעים לשערך קבוע M בשני שלבים: שלב השערוך שבו מחשבים את הערך של M על 10K דגימות ראשוניות (ניתן להראות כי עבור דוגמא נתונה M זה האקספוננט של לוג'יט הערך של D עבור דגימה זו). אחר כך בשלב הדגימה הם מעדכנים את הערך של M אם מתקבל ערך גבוה יותר של M עבור אחת הדגימות. זה עלול להוביל לשערוך יתר של הסתברויות קבלת דגימות שקדמו לעדכון של M אך לטענת המאמר עדכון של M לא קורה באופן תדיר בפועל.

בנוסף המאמר מציין כי ל-RS יש בעיה לדגום מרחבים בעלי מימד גבוה כי ההסתברות לקבלת דגימה t היא מאוד קטנה. המחברים מציעים טריק יפה (שכמובן מעוות "קצת" את ההתפלגות האמיתית של הסתברויות קבלת הדגימה) כדי ״להתגבר״ על הבעיה הזו. הטריק הוא להשתמש פרמטריזציה של הביטוי עבור הסתברות קבלת הדגימה: מכניסים פרמטר q האחראי על "הרחבת" סט הערכים של הסתברות זו. כלומר אם ערך הפרמטר גבוה אז t נוטה לקבל ערכים גבוהים יחסית וכאשר ערכו של q נמוך, גם t נוטה להיות נמוך ורוב הדגימות נדחות. בסוף עושים אופטימיזציה על הערך של פרמטר זה.

הישגי מאמר:

המחברים הצליחו לשפר את איכות התמונות המגונרטות עי״ GAN עם השיטה שלהם. ההשוואה בוצעה מול SAGAN שהיה SOTA על יצירת תמונות (מאומן על Imagenet) לפני כשנתיים.

מטריקות השוואה:

Frechet Inception Distance, Inception Score.

נ.ב. 

מאמר עם רעיון מבריק. למרות התוצאות המרשימות, חסרות בו הוכחות ריגורוזיות של ההנחות שלהם ומקווה שיבואו בהמשך. 

#deepnightlearners

הפוסט נכתב על ידי מיכאל (מייק) ארליכסון, PhD, Michael Erlihson.

מיכאל עובד בחברת סייבר Salt Security בתור Principal Data Scientist. מיכאל חוקר ופועל בתחום הלמידה העמוקה, ולצד זאת מרצה ומנגיש את החומרים המדעיים לקהל הרחב.