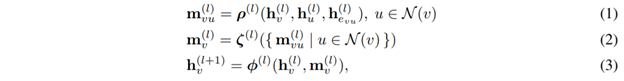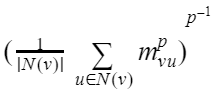DeeperGCN: All You Need to Train Deeper GCNs (סקירה)

סקירה זו היא חלק מפינה קבועה בה אנו סוקרים מאמרים חשובים בתחום ה-ML/DL, וכותבים גרסה פשוטה וברורה יותר שלהם בעברית. במידה ותרצו לקרוא את המאמרים הנוספים שסיכמנו, אתם מוזמנים לבדוק את העמוד שמרכז אותם תחת השם deepnightlearners.

לילה טוב חברים, היום אנחנו שוב בפינתנו deepnightlearners עם סקירה של מאמר בתחום הלמידה העמוקה. היום נבחר לסקירה המאמר שנקרא:

DeeperGCN: All You Need to Train Deeper GCNs

פינת הסוקר:

    המלצת קריאה מאופיר: לכל המתעניינים ברשתות נוירונים גרפיות, גם אם לא תחום העיסוק העיקרי שלהם – יתכן והמאמר יהיה שימושי גם לתחום הבעיה שלהם

    בהירות קריאה: גבוהה

    רמת היכרות עם כלים מתמטיים וטכניקות של ML/DL הנדרשים להבנת המאמר: היכרות עם מושגי יסוד של DL, המאמר כולל מיני-סקירה על GNNs

    יישומים פרקטיים אפשריים: הטכניקות המוצגות במאמר מאפשרות שיפור והעמקה של רשתות נוירונים גרפיות באופן כללי, ואינן מוגבלות לארכיטקטורה ספציפית

פרטי מאמר:

    לינק למאמר: זמין להורדה.

    לינק לקוד: זמין להורדה.

    פורסם בתאריך: 13/6/20, בארקיב.

    הוצג בכנס: גרסה מוקדמת של המאמר הוצגה בעל פה ב-ICCV2019.

תחומי מאמר:

• רשתות נוירונים גרפיות (GNNs)

כלים מתמטיים, טכניקות, מושגים וסימונים

• פונקציות אגרגציה (Aggregation functions)
• קשרים שיוריים (Residual connections)
• נורמליזציית הודעה (Message normalization)

קישורים להסברים טובים על מושגי יסוד במאמר:

• פונקציות אגרגציה
• קשרים שיוריים
• נורמליזציה
• מבוא על רשתות נוירונים גרפיות
• דיון על הקשיים בהעמקת רשתות נוירונים גרפיות, נכתב לפני פרסום המאמר הנ"ל

מבוא והסבר כללי על תחום המאמר:

רשתות נוירונים גרפיות (נקראות גם גיאומטריות, GNNs) הן רשתות נוירונים שפועלות על גרפים. כלומר, על אובייקטים (קודקודים ותכונותיהם) והאינטראקציות ביניהם (קשתות ותכונותיהן). כיום, מרבית ה-GNNs עובדות בעזרת קונבולוציות מוכללות יותר מאשר קונבולוציות ב-CNNs. הקונבולוציה של קודקוד מסוים היא בעצם פונקציה על גבי הודעות מכל השכנים שלו (ומעצמו, ובגלל זה בחלק מה-GNNs מוסיפים לולאות עצמיות לכל קודקוד כדי לפשט את התהליך). זאת, כאשר הכמות שלהם ואפילו "סוג השכנות" שלהם מוגדרים על ידי מבנה הגרף, ויכול להשתנות בין גרפים שונים ובין קודקודים שונים בגרף נתון. כל עדכון שנובע מקונבולוציה כזו מהווה שכבה אחת של ה-GNN.

לכן, בעוד שקונבולוציה ב-CNN היא פעולה מאוד מוגדרת וקבועה, ב-GNN קונבולוציה אחת יכולה להיות בעלת צורה שונה לגמרי מהשנייה (בשל כמות שכנים וסוגי קשתות שונות המובילות אליו). אפילו בתוך אותו הגרף יכולים להיות הרבה צורות קונבולוציה שונות. כשמתגברים על הבעיות הנובעות מכך, GNNs יכולות לעבוד על מגוון רחב של סוגי אינטראקציות במידע, ש-CNNs לא יכולות להתמודד איתם. דוגמה אחת היא שב-CNNs אין אופציה לכמות משתנה של פיקסלים שמשפיעה על ערכיהם של פיקסלים באותה השכבה. דוגמה נוספת היא שב-CNN הדרך היחידה למספר סוגי אינטראקציות היא בעזרת מספר channels, ודרך זו מרחיבה את כמות הפיצ'רים של הפיקסל, בעוד שב-GNN ניתן לעדכן בעזרת קשת הכוללת מספר פיצ'רים פיצ'ר ספציפי בפיקסל.

אז איך בעצם מתגברים על הבעיות האלו? משתמשים בפונקציה שהיא חסינה לשינויי גדלים ופרמוטציות בקלט (כלומר, שינוי סדר ההודעות מהשכנים השונים לא ישפיע על פלט הפונקציה). הפונקציות הבסיסיות ביותר ששימשו לכך הן max,sum,mean. המאמר מציע להשתמש בפונקציות מורכבות וכלליות יותר , בשביל להוסיף גמישות למערכת ולטפל במגבלות הפונקציות הקלאסיות, שיפורטו בהמשך הסקירה. בנוסף, לבעיות סיווג ורגרסיה על הגרף כולו משתמשים ב-pooling שדומה ברעיונו לזה של CNNs.

וכעת, כשאנו מבינים את העקרונות של GNNs, נשאלת השאלה למה הן עד כדי כך מעניינות. ובכן, התשובה היא שבגלל שהן למעשה מהוות את ההכללה האולטימטיבית לכל בעיית מידול, מכיוון שאפשר להמיר כל קלט הכולל תלות בין הפרמטרים השונים לגרף, ולהריץ עליו GNN:

• תמונות? הפיקסלים הם הקודקודים, וישנה קשת בין כל זוג פיקסלים צמוד (או אפילו ייצוג יותר מורכב).
• טקסט? מילה יכולה להיות קודקוד, עם קשת בין זוג מילים עוקבות, עם האפשרות להוסיף (כולל תוך כדי תהליך האימון) קשתות בין אזורים רלוונטיים בטקסט.
• סדרות עיתיות? כמו בטקסט, כל נקודת זמן היא קודקוד, עם קשתות בין זמנים צמודים וזמנים נוספים שמבחינתנו אמור להיות ביניהם קשר.

הסבר טכני על קונבולוציות בגרפים (שילוח הודעות):

לפעולת קונבולוציה בגרפים יש 3 שלבים:

1. יצירת ההודעה מכל קודקוד u לקודקוד שכן v, אשר תלויה בוקטורי התכונות h של הקודקודים u ו-v ושל הקשת ביניהם e(u,v) (דהיינו, האינטראקציה ביניהם). 
2. אגרגציה על פני כל ההודעות מהקודקודים השכנים. זה בעצם השלב שבו חייבים להשתמש בפונקציה שיכולה לקבל גדלי קלטים שונים ולהיות חסינה לפרמוטציות.
3. פונקציית העדכון, שקובעת איך התוצר של פונקציית האגרגציה מעדכן את ערך הקודקוד המועבר לשכבה הבאה.

ראוי לציין שאמנם אין ציון לכך במאמר, אבל אפשר תיאורטית לבצע תהליך דומה לעדכון נתונים של קשתות.

כמו כן, שלבים 1 ו-3 יכולים להכיל רשת נוירונים כשלעצמם, בעיקר ארכיטקטורות טבלאיות (כשמניחים שהפיצ'רים עצמם בלתי תלויים).

תמצית המאמר:

המאמר מציג מספר טכניקות חדשות עבור GNNs, אשר מאפשרות להעמיק את הרשתות מבלי לסבול מבעיות כמו over-smoothing, overfitting ו-vanishing gradients, אשר נגרמות בין היתר משימוש בפונקציות אגרגציה קלאסיות כדוגמת max/sum/mean.

בניגוד ל-overfitting ו-vanishing gradients שמוכרים לנו בתחומים אחרים של למידה עמוקה, over-smoothing הינה תופעה ייחודית ל-GNNs הנובעת משימוש בפונקציות האגרגציה הקלאסיות למשך שכבות מרובות. נתאר זאת על ידי דוגמה של שימוש בפונקציה mean. דמיינו גרף עם ערכים רנדומליים לקודקודים, ופונקציית יצירת הודעה שהיא הזהות. כלומר, בכל שכבה הערך של קודקוד יתעדכן לממוצע הערכים שלו ושל שכניו. כעבור שכבות רבות, הערך בכל קודקודי הגרף ישאף לאותו הערך – ממוצע הערכים המקורי בגרף, תוצאה לא שימושית במיוחד. תיאורטית, ניתן להגיע לבעיה דומה ב-CNNs אם היינו משתמשים בקרנלי מיצוע בלבד.

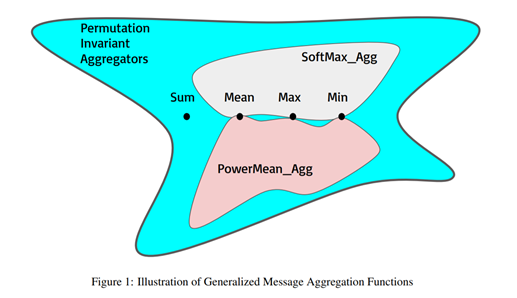
• פונקציות אגרגציה חדשות – במאמר מוצגות שתי פונקציות אגרגציה חדשות, SoftMax (מותאם) ו-PowerMean, כאשר שתיהן מהוות הכללות של  max/sum/mean, כאשר בשתיהן יש היפרפרמטר (שאפשר כעיקרון לאמן גם אותו בתהליך האימון) שקובע את ההתנהגות בפועל של הפונקציה.
  1. אגרגציית SoftMax עם היפרפרמטר בטא:
  2. אגרגציית PowerMean עם היפרפרמטר p:

1. 1. בנוסף, הקשר בין שיטות האגרגציה השונות מוצגות בתרשים הבא:

• שיפור על גבי שימוש בקשרים שיוריים. במחקרים קודמים השתמשו בסדר הפעולות GraphConv→Normalization→ReLU→Addition, אך במאמר הנ"ל מצאו כי הסדר Normalization→ReLU→GraphConv→Addition (מבצעים את הנורמליזציה והאקטיבציה לפני הקונבולוציה) מוביל לתוצאות עדיפות. הסיבה שניתנה לכך על ידי הכותבים היא שבגלל שהטווח של הפונקציה השיירית הוא בין אינסוף למינוס אינסוף, פונקציית אקטיבציה כמו ReLU פוגעת ביכולת הייצוג של מודלים עמוקים. משתמשים ספציפית ב-ReLU בגלל שפונקציות האגרגציה במאמר דורשות ערכים אי-שליליים.
• הוספת נורמליזציה להודעה. בנוסף ל-BatchNorm ו-LayerNorm שניתן להשתמש בהן ב-GNNs, הכותבים מציעים שכבת נורמליזציה ל-message עצמו לקודקוד מסוים, ביחס לגודלו של וקטור ההודעה.

הסבר על שיטות נרמול ב-GNNs: יצירת batch ברשתות נוירונים גרפיות מתרחשת על ידי איחוד של כמה גרפים נפרדים לגרף יחיד גדול (כלומר, הגרפים המקוריים הם תתי-גרפים נפרדים לחלוטין בתוכו) שהפעולות מתבצעות עליו, ללא שום קשתות שמחברות בין הגרפים השונים בו, מה שמוביל לכך שבמהלך הקונבולוציות אין השפעה של תתי-הגרפים אחד על השני. לפיכך, BatchNorm מבצעת נורמליזציה של הפיצ'רים לאותו גרף מאוחד, ו-LayerNorm מבצעת נורמליזציה לפיצ'רים של הגרף גרף באחת השכבות של ה-GNN. כמו כן, אם ה-GNN משתמש ברשת נוירונים פנימית בתור פונקציית יצירת ההודעה או העדכון, ניתן להשתמש גם בעבורה בטכניקות האלה באופן פנימי. 

דאטאסטים:

ognn-proteins, ogbn-arxiv, ogbg-ppa ,ogbg-molhiv, הכוללים משימות של ניבוי על קודקודים וניבוי על גרפים.

הישגי המאמר:

המאמר מספק כלים הניתנים לשימוש בכל רשת נוירונים גרפית, שיאפשרו יצירת רשתות עמוקות יותר בעלות יכולות ייצוג עדיפות. אלו, בתורן, יוכלו לפתור בעיות מסובכות יותר ראשית בדומיינים חריגים (בימינו, בכל אופן) ויתכן בהמשך בדומיינים קלאסיים יותר גם כן.

כמו כן, הכלים המוצעים הצליחו להביא שיפור על גבי תוצאות SOTA בדאטאסטים שנבדקו, 0.2% עד ל-7.8%, כתלות בדאטאסט.

נ.ב: באתר של המאמר מוצג יישום של GNN של הכותבים לסגמנטציה בתמונות, אז יכול להיות מעניין לאנשי ה-CV.

#deepnightlearners

הפוסט נכתב על ידי אופיר יזרעאלב.

אופיר עובד ב-Dell EMC בתור data scientist במקביל ללימודי תואר שני בדאטא סיינס וביואינפורמטיקה באוניברסיטת בן גוריון ומתעניין בדאטא סיינס ב-irregular domains כגון רשתות נוירונים גרפיות ורשתות נוירונים בינאריות.