Gradient Descent with Early Stopping is Provably Robust to Label Noise for Overparameterized Neural Networks (סקירה)

סקירה זו היא חלק מפינה קבועה בה אני סוקר מאמרים חשובים בתחום ה-ML/DL, וכותב גרסה פשוטה וברורה יותר שלהם בעברית. במידה ותרצו לקרוא את המאמרים הנוספים שסיכמתי, אתם מוזמנים לבדוק את העמוד שמרכז אותם תחת השם deepnightlearners.

לילה טוב חברים, היום אנחנו שוב בפינתנו deepnightlearners עם סקירה של מאמר בתחום הלמידה העמוקה. היום בחרתי לסקירה את המאמר שנקרא:

Gradient Descent with Early Stopping is Provably Robust to Label Noise for Overparameterized Neural Networks 

פינת הסוקר:        

       המלצת קריאה ממייק: חובה לאלו שרוצים להבין את התהליכים המתרחשים במהלך אימון של רשתות נוירונים, לשאר מומלץ לעבור על המסקנות בלבד.

       בהירות כתיבה: בינונית.

       רמת היכרות עם כלים מתמטיים וטכניקות של ML/DL הנדרשים להבנת מאמר: הבנה עמוקה בחדוו"א מתקדם ובתורת האופטימיזציה.

      יישומים פרקטיים אפשריים: מאמר תיאורטי שעשוי לעזור לשפר את תהליכי האימון של רשתות נוירונים.

פרטי מאמר:

      לינק למאמר: זמין כאן

      לינק לקוד: זמין כאן

      פורסם בתאריך: 03.07.2019, בארקיב

      הוצג בכנס: ICML2019

תחום מאמר: 

• חקר שיטות אופטימיזציה לאימון של רשתות נוירונים

כלים מתמטיים, מושגים וסימונים:

• Gradient Descent – GD
• מטריצת קווריאנס של רשת נוירונים
• מטריצת קרנל של רשת נוירונים

תמצית מאמר:

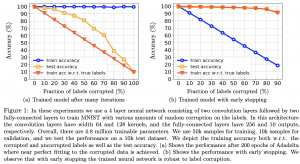
המאמר טוען (ומוכיח ריגורוזית) כי עצירה מוקדמת של אימון (באמצעות gradient descent) של רשתות נוירונים overparameterized תורמת לרובסטיות של הרשת המאומנת ללייבלים רועשים. המאמר בעצם מוכיח שבאיטרציות הראשונות שלו GD מצליח "ללמוד" איך ״נראות דוגמאות שהלייבלים שלהם נכונים״ ואם ממשיכים להריץ אותו, הרשת מתאימה את עצמה גם גם לדוגמאות בעלות הלייבלים לא נכונים. כמובן שאם זה המצב, המשך אימון של רשת אחרי השלב שהיא כבר "למדה" את הלייבלים הנכונים, פוגע בביצועיה של הרשת על טסט סט (כלומר יכולת ההכללה של הרשת יורדת).

תקציר מאמר:

למרות שמסקנות של המאמר די ברורות וקלות להבנה הוכחתן הריגורוזיות כוללות שימוש בכלים מתמטיים לא פשוטים ובהגדרות מתמטיות לא טריוויאליות. עקב כך אתמקד  בהסבר של התנאים והטענות של המשפטים האלו בסקירה זו. 

נתחיל את ההסבר מהתייחסות לארכיטקטורה של הרשת המופיעה כהנחה בכל המשפטי שהוכחו במאמר.

ארכיטקטורה של הרשת ואתחול:

כל התוצאות במאמר הוכחו לרשת דו-שכבתית (שכבה חבויה אחת) כאשר השכבה השנייה הינה קבועה ולא נלמדת (מאמנים רק את המשקלים בשכבה הראשונה). הפלט של השכבה השנייה הוא סקלר. אתחול של המשקלים הינו גאוסי (כמו ברוב המאמרים התיאורטיים ברשתות נוירונים).

הנחות על דאטהסט:

הנחה נוספת במאמר היא שהנקודות בדאטהסט הלא רועש, המתאימים ללייבלים שונים, הן מספיק רחוקות אחת מהשנייה מצד אחד ומאידך הנקודות בעלי אותם הלייבלים (קלאסים) מספיק קרובים (פרמטר ε_0) לסנטרויד של הקלאס (בעצם הגדרה במאמר טיפה מורכבת יותר ומגדירה נקודות השייכות לכל קלאס כאיחוד של כמה קלסטרים, שנקרא לו Label Set). הלייבלים מוגדרים כמספרים ממשים (!!) כאשר גם הם מספיק רחוקים אחד מהשני (פרמטר δ במאמר). דאטהסט בעל תכונות אלו נקרא באופן לא מפתיע  clusterable dataset. בואו נחשוב מה ההיגיון הטמון בהגדרה הזו. הרי ברור שככל שהסנטרואידים (מרכזים) של Label Sets של הקלאסים השונים, קרובים אחד לשני, נהיה יותר קשה לאמן רשת נוירונים (או כל מסווג מסוג אחר) המבדיל ביניהם. דאטהסט רועש מוגדר כ-clusterable dataset כאשר הלייבלים של אחוז נתון של נקודות מכל קלאס שונה ללייבלים אקראיים.

פונקציית לוס:

הרשת מאומנת לשערך את ערך הלייבל של נקודה כאשר פונקציית לוס הינה הפרש ריבועי בין פלט של הרשת לבין הלייבל של הדוגמא. קרי יש לנו כאן בעיית רגרסיה עם לוס ריבועי ולא בעיית סיווג.

מטריצת קווריאנס של רשת נוירונים:

זה מושג מרכזי במאמר שבעזרתו מוכיחים אם כל הטענות העיקריות. מטריצה קווריאנס של רשת נוירונים מוגדרת במאמר בתור מטריצה קרנל אמפירית של הרשת. נזכיר כי מטריצת קרנל של רשת נוירונים מודדת (בקירוב) את ההשפעה של צעד אחד של GD (שמעדכן את המשקלי הרשת) על ערך של פונקצית הלוס של הרשת. שערוך של ״מידת השפעה״ זו מתבצע תוך שימוש בקירוב לינארי של פונקצית לוס שהופך למדויק יותר ככל שגדלי השכבות של הרשת גדולות יותר.

כאמור אם יש לנו שני קלסטרים של נקודות (ולא רועשים) בעלי לייבילים שונים שקרובים אחד לשני אז רשת ״צריכה לעבוד קשה״ בשביל להבחין ביניהם (או במילים אחרות "לבנות" משטח המפריד בין הקלסטרים). אז מטריצת קווריאנס C באה לעזור לנו לכמת את היכולת הזו (הבחנה בין נקודות בעלות לייבלים שונים) של רשת נוירונים נתונה וסט של מרכזי קלאסטרים (סנטרואדים) נתון עבור כל לייבל. המאמר מראה כי ניתן לעשות זאת באמצעות condition number (יסומן בהמשך ב- cond) של C. אזכיר כי condition number של מטריצה מוגדר כיחס בין ערך העצמי הגדול ביותר לבין הערך העצמי הקטן ביותר של המטריצה. ככל ש-cond של מטריצת קווריאנס של הרשת נמוך יותר, אז קל יותר לרשת להבחין בין קלאסטרים שונים. 

פינת האינטואיציה: נניח כי יש שני מרכזים של קלסטרים של דוגמאות, הנושאים לייבלים שונים, נמצאים באותה נקודה. קל לראות שבמקרה הזה למטריצת קווריאנס יהיו שורות תלויות כלומר יהיה לה ע״ע 0. לכן cond שלה יהיה אינסוף שמסתדר עם טענה המנוסחת למעלה. 

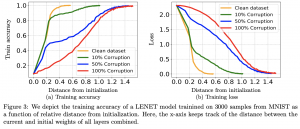
טענה עיקרית 1 של המאמר: בהינתן דאטהסט עם אחוז לייבלים רועשים נמוך מספיק, וגודל השכבה הנלמדת מספיק גדול, קרי (O(cond^4 * K^2 ,קיים קצב למידה (שהוא גם תלוי ב-cond של מטריצת קווריאנס) שעבורו, אחרי מספר צעדי GD, הרשת תלמד לזהות נכון את הלייבלים של כל הדוגמאות בדאטהסט. K מסמן את מספר הקלאסטרים ב-label set (אזכיר שכל label set מורכב מכמה קלסטרים של דוגמאות). מספר צעדי GD עד ההגעה לזיהוי מלא של כל הנקודות הלא רועשות הוא (O(K. בנוסף המרחק המקסימלי בין משקלי האתחול של רשת לבין המשקלים בכל האיטרציות של אימון (עד ההגעה למצב שהרשת מזהה נכון את כל הדוגמאות עם הלייבלים הלא רועשים) יהיה נמוך יחסית כלומר הרשת ״תטייל״ בסביבה די קטנה סביב משקלי האתחול במהלך האימון כדי לזהות נכון את הלייבלים הנקיים. 

טענה עיקרית 2: עכשיו נשאלת השאלה מה קורה אם אנחנו לא עוצרים את האימון מוקדם וממשיכים לאמן את הרשת עם GD. המשפט העיקרי השני במאמר נותן מענה לשאלה הזו. המשפט הזה מוכיח שתחת אותם התנאים על ארכיטקטורת הרשת ועל מבנה של דאטהסט, בשביל לתת דיוק של 100% על דאטהסט עם לייבל רועש אחד (לזהות נכון את כל הדוגמאות כולל זו נושאת הלייבל הרועש) המרחק שהמשקלים של הרשת צריכים לעבור (קרי המרחק בין המשקלים ההתחלתיים לבין אלו של הרשת המאומנת) צריך להיות לפחות δ/ε_0, כאשר המונה מהווה חסם על המרחק בין ערכי ההלייבלים השונים, והמכנה מתאר את הרדיוס המקסימלי של הקלסטרים של אותם הלייבלים. ככל שהקלסטרים של דוגמאות יותר גדולים (המכנה עולה) אז המרחק מתקצר (הקלסטרים יותר מרוחים וקל למצוא וקטור משקלים המסווג נכון את הדוגמא עם הלייבל הרועש). כאשר המרחק בין ערכי הלייבלים עולה (המונה עולה) המרחק ש״משקלים צריכים לעבור״ מתארך (״מכריחים את הרשת לטעות גם כשיש לה ביטחון גבוה״). הכל תחת אתחול גאוסי של המשקלים.

כלים מתמטיים המשמשים להוכחות:

המאמר משתמש ביקוביען J של מיפוי הממודל באמצעות הרשת (עבור דאטהסט נתון) בשביל לנתח את מטריצת קווריאנס של הרשת. המחברים הציגו את השארית הרועשת (הפרש בין פלט של רשת לבין לייבל רועש) כסכום של השארית הנקיה והרעש באותו לייבל רועש. לאחר מכן הם הוכיחו שהשארית הנקיה ״מכוסה״ ע״י תת-מרחב של מרחב העמודות של J המתאים לערכים סינגולריים גדולים של J. זה למעשה מאפשר לרשת ללמוד את הלייבלים הנקיים במהירות (גרדיאנטים חזקים). לעומת זאת ״הרעש בלייבל״ עצמו מכוסה עי״ תת-מרחב המתאים לערכים סינגולריים קטנים ששמקשה על האימון של הלייבלים הרועשים (גרדיאנטים חלשים). לדעתי זו מסקנה מאוד חזקה.

דאטהסטים: MNIST, CIFAR10 

נ.ב. מאמר מאוד חשוב העוזר להבין את האופן שבו רשתות ״לומדות״ את הדאטה.

#deepnightlearners

הפוסט נכתב על ידי מיכאל (מייק) ארליכסון, PhD, Michael Erlihson.

מיכאל עובד בחברת הסייבר Salt Security בתור Principal Data Scientist. מיכאל חוקר ופועל בתחום הלמידה העמוקה, ולצד זאת מרצה ומנגיש את החומרים המדעיים לקהל הרחב.